Matematik
Från Rilpedia


| Matematiska begrepp |
|---|
Matematik (av grekiska máthema, "vetenskap") är läran om abstrakta kvantiteter, strukturer och mönster. Matematiken består av metoder för att beskriva och analysera abstrakta samband, och kunskap i form av redan härledda resultat. Viktiga områden är aritmetik, talteori, algebra, analys, geometri, topologi, mängdteori och statistik, bland många andra.
Matematiken är helt abstrakt och skiljer sig på så sätt från naturvetenskap. Den är inte empirisk prövbar, utan bygger på axiom, och därför är den enligt vissa definitioner ingen vetenskap. Dock används den inom flera vetenskaper - huvudsakligen, men inte enbart, naturvetenskapliga sådana - som ett verktyg för att formulera och lösa problem.
Innehåll |
Matematiska begrepp

Nya matematiska begrepp införs med en definition, som beskriver exakt vad begreppet står för, utifrån begrepp som redan är definierade. Här presenteras några allmänna begrepp som är grundläggande i alla matematiska delområden.
En mängd är en samling objekt, till exempel en samling tal, som kan vara ändligt eller oändligt många. En mängd som inte innehåller några objekt kallas den tomma mängden. Mängder kan också innehålla andra mängder, delmängder. De studeras mer ingående i mängdteori.
Ett tal är ett objekt som representerar värdet på en storhet eller kvantitet. De naturliga talen (1, 2, 3...) är en mängd av tal som används för att räkna hela föremål. Genom matematiska operationer kan man definiera nya talmängder. Naturliga tal tillsammans med negativa heltal (till exempel -1) blir heltal, som tillsammans med bråk (till exempel ½) blir rationella tal.
De rationella talen bildar tillsammans med algebraiska tal (till exempel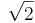 ) och transcendenta tal (till exempel π (pi) och e (Eulers konstant) de reella talen, som med imaginära tal (som mäts med den imaginära enheten i) blir komplexa tal.
) och transcendenta tal (till exempel π (pi) och e (Eulers konstant) de reella talen, som med imaginära tal (som mäts med den imaginära enheten i) blir komplexa tal.
En operation är en handling då en eller flera operander, till exempel tal, förändras enligt ett särskilt mönster, en operator, och ger ett resultat. De mest grundläggande operationerna är räknesätten - addition, subtraktion, multiplikation och division.
En parameter är ett tal som skrivs med en särskild symbol. En parameter är antingen en variabel som ändrar värde, eller en konstant som alltid har samma värde. En matematisk konstant är en konstant med en bestämd, matematisk definition. Bland de viktiga matematiska konstanterna finns talen 0 och 1, men också mer invecklade tal som de ovan nämnda π och e. Ett matematiskt uttryck är en samling tal och/eller parametrar som är sammanlänkade med operatorer så de ger ett entydigt resultat.
En ekvation är ett påstående om att två matematiska uttryck har samma värde. En ekvation skrivs med likhetstecken: ekvationen x=5 innebär att variabeln x har värdet 5. Ett ekvationssystem består av flera ekvationer som är giltiga samtidigt. Några vanliga typer av ekvationer är differentialekvationer och diofantiska ekvationer. En variant på ekvationen är en olikhet, alltså ett påstående om att två matematiska uttryck är olika, till exempel triangelolikheten, som säger att varje sida i en triangel är kortare än summan av de två andra.
En funktion är en variabel som är beroende av en eller flera andra variabler enligt en ekvation. Några viktiga funktioner är linjära funktioner, polynom, exponentialfunktioner och trigonometriska funktioner.
En vektor är i allmänhet en lista på tal, som är vektorns komponenter. Antalet tal är vektorns dimension. Med hjälp av ett koordinatsystem kan vektorer bilda punkter i ett vektorrum. Dessa punkter kan sättas samman till geometriska figurer. En vektor kan i stället för tal bestå av andra objekt, som följer vissa grundläggande räkneregler. Till exempel kan polynom användas som vektorer. En matris är en tabell av tal som kan beskriva ett ekvationssystem eller en linjär avbildning av vektorer från ett vektorrum till ett annat.
Matematiska delområden

Matematikens delområden är ofta svåra att särskilja både i teori och tillämpning, och undervisas i samma kurs upp till gymnasienivå. På högskolan brukar delområdena separeras till olika kurser, men det brukar vara först efter kandidatexamen eller motsvarande som en matematikstudent specialiserar sig på något delområde.
Den mest grundläggande matematiken är aritmetik, även kallad räknelära, som beskriver räknande och räknesätten, med övning i huvudräkning, avrundning och överslagsräkning. En teoretisk utbyggnad är talteori som definierar olika typer av naturliga tal, som primtal och perfekta tal.
Geometri beskriver former. Utifrån punkter, konstruerar man linjer, vinklar, och därifrån cirklar, månghörningar kroppar och andra geometriska objekt. Trigonometri beskriver förhållandet mellan vinklar. I analytisk geometri definieras ett rum utifrån ett koordinatsystem. Sentida utvecklingar är fraktalgeometri och topologi.
Algebra beskriver operationer på parametrar och andra matematiska objekt. Den kan delas in i flera nivåer - elementär algebra där variablerna står för enskilda tal, linjär algebra där de står för vektorer och matriser, abstrakt algebra där de står för andra algebraiska strukturer och universell algebra.
Matematisk analys utgår från differentialer och gränsvärden, för att beräkna derivator - förändringar av en funktions värde, och integraler - kontinuerliga summor av en funktions värde. Analys kan kombineras med linjär algebra till vektoranalys och differentialgeometri. Komplex analys beskriver differentiering av komplexa funktioner. En viktig tillämpning är lösning av differentialekvationer, som beskriver förhållandet mellan en funktion och dess derivator.
Diskret matematik är operationer med heltal. En viktig gren är kombinatorik som beskriver antal kombinationer och permutationer.
Sannolikhetsteori och matematisk statistik beskriver operationer med stokastiska variabler, som ger ett slumpmässigt utfall enligt en sannolikhetsfördelning.
Historik
- Huvudartikel: Matematikens historia

Matematikens historia sträcker sig från förhistorisk tid till nutid. Den innefattar – utöver ett kontinuerligt ansamlande av matematisk kunskap – utveckling av arbetsmetoder och upptäckter av nya tillämpningsområden, och är tätt sammanvävd med naturvetenskapens, teknikens och filosofins historia.
Från sitt ursprung i den grundläggande räknekonsten har den matematiska kunskapen och metodiken utvecklats under loppet av årtusenden. Framstående matematiska kulturer fanns bland annat under antiken i Babylonien och Grekland, och under medeltiden i mellanöstern. Utvecklingen kom dock att explodera i det eftermedeltida Europa, väsentligen i samband med den vetenskapliga revolutionen, och i dag bedrivs mer matematisk forskning än någonsin tidigare.
Egenskaper och metodik
Matematiker studerar tal, geometriska figurer, och många andra abstrakta föremål som kan vara mer eller mindre svåra att få en intuitiv uppfattning om. Målet är i allmänhet att försöka upptäcka mönster och sammanhang. Mönstren sammanfattas i form av regler som, förutom att ge en förståelse av de objekt som studeras, kan användas för att lösa nya problem. För att reglerna ska vinna erkännande krävs det också av matematikerna att de genom rigoröst logiskt resonemang bevisar att reglerna verkligen stämmer.
Matematisk notation
Den matematiska notationen består av symboler och konventioner som låter matematiker uttrycka idéer på ett koncist och exakt sätt.
För att skriva naturliga tal använder man talsystem och siffror. Tillsammans med dessa används matematiska symboler för att beskriva andra talformer (bråkstreck, procent, promille och decimaltecken för rationella tal, minustecken för negativa tal, rottecken för algebraiska tal etc), de olika räknesätten och andra operationer.
Formell matematisk terminologi
Matematikerna har under århundradena utvecklat ett språk för att uttrycka sina resultat och kommunicera med varandra. Det matematiska språket är nödvändigt, eftersom naturliga språk sällan är exakt nog. Detta har lett till att även vanliga ord som "om" och "öppen" har en väldigt specifik betydelse inom matematiken.
Bevisföring

Matematiken är objektiv och exakt, eftersom den bygger på logik och är oberoende av den fysiska världen. Oavsett hur starkt stöd utförda observationer ger en naturvetenskaplig teori är det i princip möjligt att nästa observation omkullkastar den, men ett matematiskt resultat är otvivelaktigt och evigt sant då det en gång bevisats.
Matematiska resultat utgörs av satser (eller teorem), antaganden som har bevisats objektivt. Ett matematiskt bevis består av ett antal steg som följer logiska inferensregler. Eftersom varje steg bara kan härleda en sanning från en annan, krävs grundläggande, uppenbara sanningar som alla andra resultat kan falla tillbaka på. Dessa sanningar kallas axiom. Det visar sig att nästan alla kända matematiska resultat kan härledas från endast en handfull axiom, de mängdteoretiska axiomen.
I praktiken följer matematiker ofta sin intuition eller experimenterar sig fram då de angriper nya problem, men det är av yttersta vikt att resultaten kan bevisas formellt, då det finns många exempel på "intuitivt sanna" antaganden från matematikens historia som visat sig vara felaktiga vid grundligare undersökning. Strävan att undanröja möjligheten till sådana fel var en bidragande orsak till utvecklingen av den matematiska formalismen som konsoliderades i början av 1900-talet.
Estetik
Matematiker använder ibland ordet "vackert" för att beskriva till exempel ett bevis eller ett samband. Till skillnad från de flesta andra uttryck inom matematiken är det svårt att specifiera exakt vad som menas med detta, men det kan till exempel innebära att flera olika områden som till en början kan tyckas åtskilda binds samman, en metod som lätt går att använda på många olika problem, eller ett bevis som drar långtgående slutsatser från ett fåtal förutsättningar. Typexemplet på ett vackert uttryck är följande
som kopplar samman Eulers konstant e, som är viktig inom analys, imaginära enheten i från komplex analys, π från geometrin samt 1 som är grunden för de naturliga talen och 0.
Matematikens filosofi
Matematiken beskrivs ibland som en formalvetenskap, ibland inte som vetenskap alls.
Precis vad matematik är, och hur matematiska sanningar och begrepp relaterar till den fysiska världen och det mänskliga sinnet, är omtvistade frågor som studeras inom matematikfilosofin, där det finns flera konkurrerande perspektiv eller "skolor". En av dessa skolor är platonismen eller realismen, som hävdar att alla kända och okända matematiska objekt existerar i en parallell idévärld. Matematiken ses som utforskandet av den världen, matematiska resultat som upptäckter. Andra menar att matematiken delvis eller helt och hållet är konstruerad av människor. Den tyske matematikern Leopold Kronecker (1823-1891) anmärkte att "Gud skapade heltalen. Allt annat är människans verk".
Den dominerande uppfattningen bland moderna matematiker är den formalistiska, det vill säga matematik ses som härledningen av teorem i något inferenssystem, utifrån några axiom. Axiomen och inferensreglerna ses inte som naturlagar, utan. Frågan är varför vissa axiom ger sanningar som verkar stämma med den fysiska världen. Formalismen säger ingenting om de matematiska objektens verklighet. Däremot löser den problem, till exempel satser som inte kan avgöras.
Bland andra Eugene Wigner påpekar matematikens "orimliga effektivitet" inom naturvetenskap.
Många matematiker betraktar delvis ämnet som konst. Se även metamatematik.
Studier i matematik
Matematik är ett omfattande ämne i skolor i hela världen. Det undervisas också på universitet. I akademisk utbildning är det ett obligatoriskt ämne i naturvetenskaps- och ingenjörsutbildningar.
Universiteten står idag för huvuddelen av all matematisk forskning. Matematisk forskning handlar oftast om att finna bevis för förmodanden, så att de blir teorem. En berömd matematisk facktidskrift är Acta Mathematica.
Tillämpningar
Kvantitativa vetenskaper, som naturvetenskaper, ingenjörsvetenskaper och samhällsvetenskaper, bygger på matematiska modeller. En matematisk modell generaliserar den verklighet man vill beskriva, och kan användas för att kunna göra förutsägelser.
Se även approximation och överslagsräkning.
Matematik i fysik
Fysik, den vetenskap som beskriver storheter, bygger på naturlagar som formulerats som matematiska ekvationer. Fysiken har till stor del utvecklats parallellt med matematiken.
Numerisk analys
Numerisk analys, eller beräkningsvetenskap, är läran att lösa matematiska problem med algoritmer. Genom datorer har den numeriska analysen blivit ett viktigt tekniskt redskap.
Källor
- Saint Andrews Universitet - An overview of the history of mathematics
- Christer Kiselman - Vad är matematik?
- Att forska i matematik
Se även
- Matematikens historia
- Matematiker
- Matematikterminologi
- Matematisk statistik
- Mängdteori
- Talteori
- Pseudomatematik
Externa länkar
- Christer Kiselman - Vad är matematik?
- Tord Ganelius - Introduktion till matematiken
- Saint Andrews Universitet - Matematiker som föddes eller dog idag
- Saint Andrews Universitet - Kvinnliga matematiker
- Wolfram Mathworld mathematical resources