Permutation
Från Rilpedia
- Denna artikel handlar om den matematiska termen permutation. För den juridiska termen, se Permutation (juridik).
En permutation är ett ordnat urval av element i en mängd, som skiljer sig från en kombination genom att den tar hänsyn till i vilken ordning elementen i urvalet kommer. abc och bca är således inte samma permutation, men samma kombination.
Antalet permutationer av en mängd innehållande n stycken element är n!, där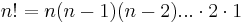 
och utläses "n-fakultet". Detta gäller eftersom det för det första elementet man väljer finns n möjliga val, för nästa element (n-1) element kvar att välja från, för tredje elementet (n-2), osv. till och med det sista elementet som kan "väljas" på endast ett sätt.
Mängden C = {a,b,c} kan alltså permuteras på 3!=6 sätt: abc, acb, bac, bca, cab, cba.
Om man ur en mängd med n element skulle välja ut r av dessa och sedan permutera urvalet, finns det n! / (n − r)! permutationer av dessa. För detta har man infört skrivsätten P(n,r), nPr och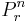 
.
Detta gäller självklart också i specialfallet n = r, eftersom P(n,n) = n! / (n − n)! = n! / 0! = n!, vilket gäller eftersom 0! är en tom produkt, som alltid är lika med 1.
En permutation av mängden M kan ekvivalent definieras som en bijektiv avbildning från M till sig själv. Mängden av permutationer på M bildar då en grupp under sammansättningsoperatorn, den symmetriska gruppen på M.
Begreppet permutationer används bland annat inom sannolikhetsberäkningar och talteori.
Se även
.svg){kind=small}
Denna artikel om kombinatorik eller diskret matematik är bara påbörjad. Du kan hjälpa till genom att utöka den.
