Från Rilpedia

Kombinatorik är den del av den diskreta matematiken som behandlar problem angående antalet element i mängder. Ett exempel på kombinatoriskt problem är att bestämma antalet möjligheter att välja k element bland n givna.

Ett exempel kan vara att räkna ut hur många olika ordningsföljder en 52-korts kortlek läggas i. Lösningen i det fallet är 52! (utläses "fakulteten av 52" eller "52 fakultet"), alltså 52·51·50· ··· ·3·2·1 vilket blir cirka 8·10⁶⁷, eller en åtta följd av 67 nollor.

Kombinatoriska problem kan ofta jämställas med problemet att fördela ett antal saker i olika lådor. Beroende på egenskaperna hos sakerna och lådorna, så blir funktionerna för att räkna ut hur många kombinationer det finns olika.

I följande tabell så kallar vi antalet saker för n, antalet behållare för m och Stirlingtalet av andra graden för S(m, n).

Sakerna är unika	Behållarna är unika	Behållare får vara tomma	Antal kombinationer
Ja	Ja	Ja	mn
Ja	Ja	Nej	n!·S(m, n)
Ja	Nej	Ja	S(m, 1) + S(m, 2) + ··· + S(m, n)
Ja	Nej	Nej	S(m, n)
Nej	Ja	Ja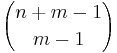
Nej	Ja	Nej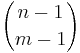

Centrala begrepp inom kombinatoriken är kombination, permutation och Dirichlets lådprincip.

Kombinatorikens verktyg är av stor betydelse inom sannolikhetslära och statistik, men den rena kombinatoriken skiljer sig från dessa två genom att den alltid behandlar exakta antal, medan de övriga två behandlar sannolikhetsfördelningar.

Med kombinatorikens hjälp kan man, utifrån korrekta grunddata, uttala sig utan osäkerhet om något. Till exempel: Det finns helt säkert minst tio svenskar som är lika långa på mikrometern när (se exempel i Dirichlets lådprincip).

Statistiken kan i stället uttrycka till exempel att 75% (Obs! Påhittad siffra) av alla svenskar är mellan 150 och 190 cm långa.

Sannolikhetsläran säger till exempel (baserat på ovanstående påstående) att om jag går ut genom dörren är sannolikheten 0.75 (= 75%) att den första person jag möter är mellan 150 och 190 cm lång.