Stirlingtal
Från Rilpedia
Stirlingtal används inom matematiken för att beskriva antalet permutationer eller partitioner av storlek m av en mängd av storlek n. Det finns två slags Stirlingtal, Stirlingtal av första slaget och Stirlingtal av andra slaget. Stirlingtalen är uppkallade efter matematikern James Stirling.
Innehåll |
Notation
Stirlingtal av första slaget betecknas ibland s(n,k) och Stirlingtal av andra slaget betecknas ibland S(n,k). En annan notation är:
Denna notation med hak- och klammerparenteser, som är analog med notationen för binomialkoefficienter, infördes av Jovan Karamata.
Stirlingtal av första slaget
Stirlingtal av första slaget, ![\left[{n \atop k}\right]](/w/images/sv.rilpedia.org/math/3/3/7/3378a24fe896ef2b8c9574dca6e96be6.png) , är antalet sätt att ordna n element i k icketomma cykler, d v s ordningar av tal som är cykliska permutationer av varandra. Om vi har mängden A = {1,2,3} kan vi från den konstruera 2 olika cykler med 3 element i varje (vi betecknar en cykel med [1,2,...,n]):
, är antalet sätt att ordna n element i k icketomma cykler, d v s ordningar av tal som är cykliska permutationer av varandra. Om vi har mängden A = {1,2,3} kan vi från den konstruera 2 olika cykler med 3 element i varje (vi betecknar en cykel med [1,2,...,n]):
Så att ![\left[{3 \atop 1}\right] = 2](/w/images/sv.rilpedia.org/math/f/8/f/f8ffcc4525d560a3d72f0ecd4cce6a89.png) . Observera alltså att [1,2,3] = [2,3,1] = [3,1,2], vi kan plocka en siffra framifrån och sätta längst bak.
. Observera alltså att [1,2,3] = [2,3,1] = [3,1,2], vi kan plocka en siffra framifrån och sätta längst bak.
Man ser att ![\left[{0 \atop 0}\right] = 1](/w/images/sv.rilpedia.org/math/2/2/e/22e0ed41fc61801a43020dd89e934018.png) , det finns ett sätt att placera inga element i noll icketomma cykler, i övrigt gäller att
, det finns ett sätt att placera inga element i noll icketomma cykler, i övrigt gäller att ![\left[{n \atop 0}\right] = 0](/w/images/sv.rilpedia.org/math/9/b/6/9b63108ee3b52a587f5f7b6404d638aa.png) (
(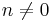 ), för det finns inget sätt att placera ut n element i noll icketomma cykler. För Stirlingtal av första slaget ser man att
), för det finns inget sätt att placera ut n element i noll icketomma cykler. För Stirlingtal av första slaget ser man att ![\left[{n \atop n}\right] = 1](/w/images/sv.rilpedia.org/math/1/a/5/1a5436e2f88c144e3d284b6069dfd57f.png) , för det finns ett sätt att placera ut n element i n icketomma cykler (varje cykel innehåller då ett element).
, för det finns ett sätt att placera ut n element i n icketomma cykler (varje cykel innehåller då ett element).
Man kan räkna ut Stirlingtal av första slaget med följande rekursiva ekvation:
Några exempel på Stirlingtal av första slaget:
| n\k | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 0 | 1 | |||||
| 1 | 0 | 1 | ||||
| 2 | 0 | 1 | 1 | |||
| 3 | 0 | 2 | 3 | 1 | ||
| 4 | 0 | 6 | 11 | 6 | 1 | |
| 5 | 0 | 24 | 50 | 35 | 10 | 1 |
Stirlingtal av andra slaget
Stirlingtal av andra slaget, 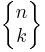 , ger antal sätt att dela in en mängd med n element i k icketomma mängder.
, ger antal sätt att dela in en mängd med n element i k icketomma mängder.
Om vi t ex har en mängd med fyra element, exempelvis A = 1,2,3,4 och vill veta på hur många sätt vi kan dela upp A i två mängder, d v s räkna ut 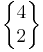 , ser vi att vi kan göra det på sju sätt:
, ser vi att vi kan göra det på sju sätt:
D v s, 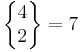 .
.
Stirlingtal av andra slaget på formen 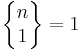 för positiva n, eftersom en mängd bara kan delas upp i en mängd med lika många element på ett sätt. Om k = 0 kan vi säga att det bara finns ett sätt att dela in en tom mängd i noll icketomma mängder, så att
för positiva n, eftersom en mängd bara kan delas upp i en mängd med lika många element på ett sätt. Om k = 0 kan vi säga att det bara finns ett sätt att dela in en tom mängd i noll icketomma mängder, så att 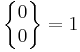 , men en icketom mängd kan inte delas upp i noll mängder på något sätt, så att
, men en icketom mängd kan inte delas upp i noll mängder på något sätt, så att 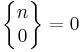 . Man inser också att det går att dela in en mängd med n element i n mängder på ett sätt, så att
. Man inser också att det går att dela in en mängd med n element i n mängder på ett sätt, så att 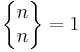 .
.
Stirlingtal av andra slaget kan räknas ut rekursivt med:
Några Stirlingtal av andra slaget är:
| n\k | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 0 | 1 | |||||
| 1 | 0 | 1 | ||||
| 2 | 0 | 1 | 1 | |||
| 3 | 0 | 1 | 3 | 1 | ||
| 4 | 0 | 1 | 7 | 6 | 1 | |
| 5 | 0 | 1 | 15 | 25 | 10 | 1 |
Relationer med Stirlingtal
Man kan se att antal möjliga cykler av en mängd är större än eller lika med antalet möjliga mängder, d v s:
Det är ganska lätt att inse att:
Man kan också koppla ihop Stirlingtalen med binomialkoefficienter: När man ska ordna n element i n − 1 cykler eller delmängder får man exakt en cykel eller delmängd som innehåller två element, och då [a,b] = [b,a] så är detta samma sak som att välja ut de två element som kommer hamna i samma delmängd eller cykel, så att:
![\left[{n \atop n-1}\right] = \left\{\begin{matrix} n \\ n-1 \end{matrix}\right\} = \begin{pmatrix} n \\ 2 \end{pmatrix}](/w/images/sv.rilpedia.org/math/9/1/e/91ea2ba490b051e9d824ad9f27fd405b.png)




![s(n,k) = \left[{n \atop k}\right]](/w/images/sv.rilpedia.org/math/5/1/7/517ef9f1bbe7c8c9109dad16e6fc878f.png)
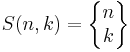
![[1, 2, 3] ~~ [1, 3, 2]](/w/images/sv.rilpedia.org/math/e/0/7/e073840340d6dc799f6d12a0b6aebe95.png)
![\left[{n \atop k}\right] = (n-1)\left[{n-1 \atop k}\right]+\left[{n-1 \atop k-1}\right]](/w/images/sv.rilpedia.org/math/d/d/c/ddc91d374c4fdf3f2b4dd8e8360f7da8.png)
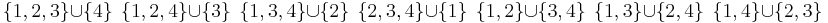
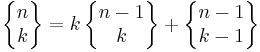
![\left[{n \atop k}\right] \geq \left\{\begin{matrix} n \\ k \end{matrix}\right\}](/w/images/sv.rilpedia.org/math/6/7/5/67537cc66ff1f1362a0f64afc59443b5.png)
![\left[{n \atop n}\right] = \left\{\begin{matrix} n \\ n \end{matrix}\right\}](/w/images/sv.rilpedia.org/math/7/e/1/7e1a2f30708a627f6556580d7e032a0d.png)