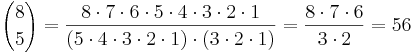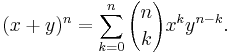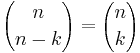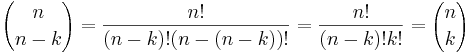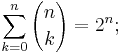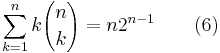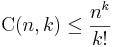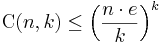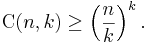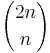Binomialkoefficient

Från Rilpedia

Texten från svenska Wikipedia

Inom matematiken definieras binomialkoefficienten 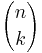${n \choose k}$ kombinatoriskt för det naturliga talet n och heltalet k som antalet oordnade urval av k olika element ur en mängd med n olika element, det vill säga antalet k-delmängder av en n-mängd. Det kan visas att detta är ekvivalent med att

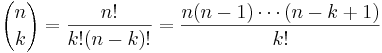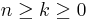
${n \choose k} = \frac{n!}{k!(n-k)!} = \frac {n(n-1)\cdots(n-k+1)}{k!}$ för $n \ge k \ge 0$

där $m!$ är fakulteten av $m$ och

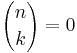${n \choose k} = 0$ för

k < 0

eller

k > n .

Den sista likheten beror på att det inte kan väljas ut ett negativt antal element ur en n-mängd, och inte heller fler än n element.

Denna algebraiska framställning generaliserades av Isaac Newton till en allmänare algebraisk definition, där det för varje reellt tal a och varje naturligt tal k sätts

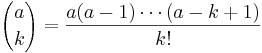${a \choose k} = \frac {a(a-1)\cdots(a-k+1)}{k!}$ .

Senare har denna definition utvidgats, genom att tillåta a att vara ett godtyckligt komplext tal.

Två exempel:

${8 \choose 5} = \frac{8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{(5 \cdot 4 \cdot 3 \cdot 2 \cdot 1) \cdot (3 \cdot 2 \cdot 1)}= \frac{8 \cdot 7 \cdot 6 }{3 \cdot 2} = 56$

Annorlunda uttryckt: antalet möjligheter att välja 5 ur 8 (8*7*6*5*4) dividerat med antalet permutationer av 5 (5*4*3*2*1) ger oss antalet sätt vi kan välja 5 ur 8, utan att ta hänsyn till varje enskild permutation.

Enligt Newtons utvidgade definition

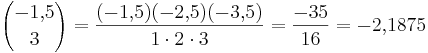${-1{,}5 \choose 3} = \frac {(-1{,}5)(-2{,}5)(-3{,}5)} {1\cdot2\cdot3} = \frac{-35}{16} = -2{,}1875$ .

Notationen 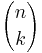${n \choose k}$ skall ha introducerats av Albert von Ettinghausen 1826 ^{[källa behövs]}, fast själva koefficienterna hade använts redan långt tidigare (se Pascals triangel).

Binomialkoefficienterna är koefficienterna i utvecklingen av potenser av binomet $x + y$ :

$(x+y)^n = \sum_{k=0}^{n} {n \choose k} x^k y^{n-k}.$

Denna utveckling är generaliserad genom binomialsatsen, vilken tillåter att exponenten n är negativ eller till och med komplex.

Binomialkoefficeinterna är viktiga inom kombinatoriken, där 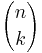${n \choose k}$ ofta skrivs C(n, k), _nC_k eller 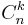$C^{k}_{n}$ , och är uttrycket för antalet sätt som det kan skapas en delmängd med k element ur en mängd med n element.