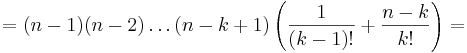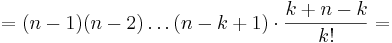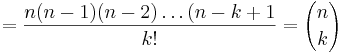Pascals triangel

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

\begin{matrix} &&&&&1\\ &&&&1&&1\\ &&&1&&2&&1\\ &&1&&3&&3&&1\\ &1&&4&&6&&4&&1 \end{matrix}

De fem första raderna i Pascals triangel

Inom matematiken är Pascals triangel en geometrisk framställning av binomialkoefficienterna i form av en triangel. Den namnges ofta efter matematikern och fysikern Blaise Pascal, men var känd utanför Europa långt före Pascals levnad.

Förenklat sett är varje ny rad ett element längre än ovanförliggande rad och varje elements värde är summan av elementen till vänster och höger ovanför (om dessa existerar). På så sätt har varje rad en etta i varje ände. Rad- och kolumnräkningen börjar båda på noll.

Så, för att beräkna det fjärde elementet på rad fem så adderar man det tredje och fjärde elementet på föregående rad.

Matematiskt sett använder man sig av Pascals identitet som säger:

{n \choose k} = {n-1 \choose k-1} + {n-1 \choose k}

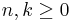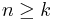där n,k \ge 0 och n \ge k med initialvärdet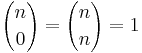 {n \choose 0} = {n \choose n} = 1

Således motsvarar första elementet i triangeln binomialen 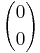{0 \choose 0} och kan alltså refereras till som rad (n + 1)

Talen i mittkolumnen kallas centrala binomialkoefficienter.

Bevis

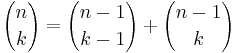
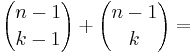
{n-1 \choose k-1} + {n-1 \choose k} =
= \frac{(n-1) \ldots [(n-1)-(k-1)+1]}{(k-1)!} + \frac{(n-1) \ldots [(n-1)-k+1]}{(k)!} =
= (n-1)(n-2) \ldots (n-k+1) \left(\frac{1}{(k-1)!} + \frac{n-k}{k!} \right) =
= (n-1)(n-2) \ldots (n-k+1) \cdot \frac{k+n-k}{k!} =
= \frac{n(n-1)(n-2) \ldots (n-k+1}{k!} = {n \choose k}


Encoder Disc (3-Bit).svg Denna artikel om kombinatorik eller diskret matematik är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Pascals_triangel"
Personliga verktyg