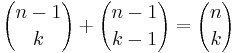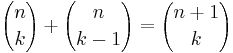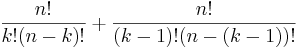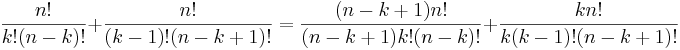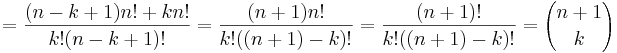Pascals identitet

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Pascals identitet, matematiskt uttryck för binomialkoefficienter, namngivet efter matematikern Blaise Pascal. Identiten säger att

{n-1\choose k} + {n-1\choose k-1} = {n\choose k}

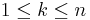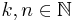där 1 \leq k \leq n, k,n\in \N.

Innehåll

Bevis

Kombinatoriskt

Pascals identitet är lätt att förstå om man betraktar den ur ett kombinatoriskt perspektiv. Eftersom 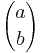{a\choose b} är antalet sätt vi kan skapa en delmängd med b element ur en mängd med a element, tecknar 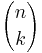{n\choose k} hur många olika distinkta delmängder med k element man kan få ur en mängd med n element.

Tag nu ett element X ur mängden med n element. För varje delmängd med k element finns då två alternativ – antingen hör X till delmängden eller så gör det inte det.

Om X tillhör delmängden, behöver man nu endast välja k-1 element bland de n-1 som återstår för att få k stycken. Detta kan göras på 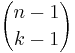n-1\choose k-1 sätt.

Om X inte tillhör delmängden, behöver man nu välja alla k element ur den n-1 element stora delmängd som innehåller alla element utom X. Det kan göras på 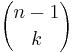n-1\choose k sätt.

Vi kan alltså dra slutsatsen att antalet sätt att skapa en delmängd med k element ur en mängd med n element är lika många som att skapa en delmängd med k-1 element ur en mängd med n-1 element plus antalet sätt man kan skapa en delmängd med k element ur en mängd med n-1 element.

Vilket skulle visas.

Algebraiskt

Vi skall visa att

{ n \choose k } + { n \choose k-1 }={ n+1 \choose k }

Vänsterledet kan skrivas om som

\frac{n!}{k!(n-k)!} + \frac{n!}{(k-1)!(n-(k-1))!}

Genom att hitta minsta gemensamma nämnare och förenkla fås

\frac{n!}{k!(n-k)!} + \frac{n!}{(k-1)!(n-k+1)!}=\frac{(n-k+1)n!}{(n-k+1)k!(n-k)!}+\frac{kn!}{k(k-1)!(n-k+1)!}
=\frac{(n-k+1)n!+kn!}{k!(n-k+1)!} =\frac{(n+1)n!}{k!((n+1)-k)!}=\frac{(n+1)!}{k!((n+1)-k)!}={ n+1 \choose k }

Vilket skulle visas

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Pascals_identitet"
Personliga verktyg