Bijektiv
Från Rilpedia
| Den här artikeln anses undermålig och kan behöva skrivas om helt för att leva upp till Wikipedias artikelstandard. Diskutera frågan på diskussionssidan och förbättra gärna artikeln. Var uppmärksam på artikelns innehåll. Motivering: Artikeln skiljer ej mellan värdemängder och målmängder |
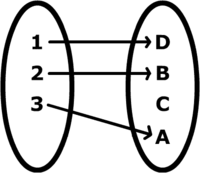
En avbildning 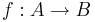 är bijektiv om det för varje värde y i avbildningens värdemängd B finns precis ett värde x i dess definitionsmängd A och vice versa. Detta innebär att en bijektiv avbildning är precis både injektiv och surjektiv. Om f är bijektiv, så säges den också vara en bijektion från X till Y.
är bijektiv om det för varje värde y i avbildningens värdemängd B finns precis ett värde x i dess definitionsmängd A och vice versa. Detta innebär att en bijektiv avbildning är precis både injektiv och surjektiv. Om f är bijektiv, så säges den också vara en bijektion från X till Y.
Begreppet är viktigt eftersom bara bijektiva funktioner kan ha inversa funktioner. Observera att även om en funktion inte är bijektiv på hela reella tallinjen kan man kan välja att bara betrakta ett intervall där funktionen är bijektiv, och definiera en invers på detta intervall. Detta har till exempel gjorts för de trigonometriska funktionerna.
Definition
Låt f vara en funktion från X till Y, det vill säga 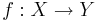 .
.
f är bijektiv, om för alla 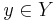 det finns exakt ett element
det finns exakt ett element 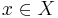 sådant att f(x) = y.
sådant att f(x) = y.
Dessa villkor kan också alternativt uttryckas:
f är bijektiv, om f är både injektiv och surjektiv.