Injektiv
Från Rilpedia
| Den här artikeln anses undermålig och kan behöva skrivas om helt för att leva upp till Wikipedias artikelstandard. Diskutera frågan på diskussionssidan och förbättra gärna artikeln. Var uppmärksam på artikelns innehåll. Motivering: Injektiv används ibland synonymt med bijektiv (och en-en eller ett-ett förekommer då också som synonymer). Detta bör utredas i samband med skilda funktionsbegrepp. |
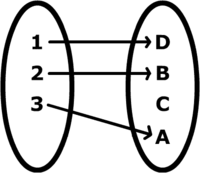
I matematik så är en injektiv funktion en funktion som avbildar skilda värden på skilda värden. Mer precist, en funktion f sägs vara injektiv om, för varje y i målmängden så finns som mest ett element x i definitionsområdet för funktionen sådant att f(x) = y.
En alternativ beskrivning är följande: f är injektiv om f(a) = f(b) medför att a = b för varje a, b i definitionsområdet.
En tredje alternativ beskrivning är: f är injektiv om a 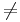 b medför f(a)
b medför f(a) 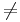 f(b), för varje a, b i definitionsområdet.
f(b), för varje a, b i definitionsområdet.
En injektiv funktion kallas även en injektion. På engelska används ibland även uttrycket one-to-one function. (Denna terminologi bör dock undvikas, eftersom det kan förväxlas med begreppet one-to-one correspondence, dvs en bijektiv funktion.)
Definition
Låt X och Z vara två mängder och f en funktion f:X->Z. Då säges f vara injektiv, eller en injektion om f(x)=f(y) implicerar att x=y. Alternativt uttryckt är funktionen injektiv om varje värde i dess värdemängd motsvaras av högst ett värde i dess definitionsmängd.
Se även
Referenser
Anders Vretblad: Algebra och geometri. Andra upplagan. 2006.