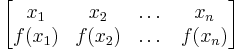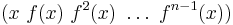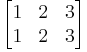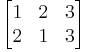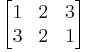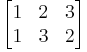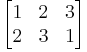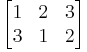Symmetrisk grupp

Från Rilpedia

Texten från svenska Wikipedia

Den symmetriska gruppen Sym(M) till en mängd M består av alla permutationer av M, d. v. s. bijektiva avbildningar från M till sig själv, med komposition (sammansättning) som gruppoperator.

De symmetriska grupperna till två mängder av samma kardinalitet är isomorfa. Man talar därför om den symmetriska gruppen på n element, och betecknar denna med S_n.

Varje grupp G är isomorf med en delgrupp till Sym(G) genom avbildningen 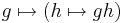$g\mapsto(h\mapsto gh)$ (Cayleys sats).

Notation

En permutation f av en ändlig mängd M kan noteras som en tabell, där första raden är en listning av M och andra raden består av bilderna av motsvarande element på första raden.

$\begin{bmatrix}x_1&x_2&\dots&x_n\\f(x_1)&f(x_2)&\dots&f(x_n)\end{bmatrix}$

En annan notation är den så kallade cykliska notationen, där varje element skrivs som en produkt av cykler

$(x\ f(x)\ f^2(x)\ \dots\ f^{n-1}(x))$

där $f n (x) = x$ . Cykler av längd ett brukar utelämnas som underförstådda.

Exempel: 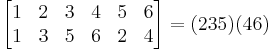$\begin{bmatrix}1&2&3&4&5&6\\1&3&5&6&2&4\end{bmatrix}=(235)(46)$ .

Nedan ges en listning av alla element i $S 3$ i de båda notationerna.

$\begin{bmatrix}1&2&3\\1&2&3\end{bmatrix}$	$\begin{bmatrix}1&2&3\\2&1&3\end{bmatrix}$	$\begin{bmatrix}1&2&3\\3&2&1\end{bmatrix}$	$\begin{bmatrix}1&2&3\\1&3&2\end{bmatrix}$	$\begin{bmatrix}1&2&3\\2&3&1\end{bmatrix}$	$\begin{bmatrix}1&2&3\\3&1&2\end{bmatrix}$
$()$	$(12)$	$(13)$	$(23)$	$(123)$	$(132)$