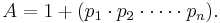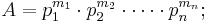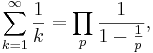Primtal
Från Rilpedia
Ett primtal är ett heltal som är större än 1 och delbart endast med sig själv och med 1.
Orddelen prim kommer av ett latinskt ord som betyder först,främst.
Ett primtal kan inte skrivas som en produkt av två eller flera heltal. Exempelvis är 7 ett primtal eftersom det inte är delbart med några andra tal än 1 och sig själv. 51 är däremot inte ett primtal eftersom 51 är lika med 3 · 17 som är primtalsfaktorer. Alltså alla positiva heltal som kan delas upp i primtalsfaktorer är inte primtal. Bland de oändligt många primtalen förekommer det att två på varandra följande udda tal är primtal, exempelvis 11 och 13 är så kallade primtalstvillingar , men man vet fortfarande inte om det finns oändligt många sådana par. Primtalens mystik och fördelning har alltid varit ett intressant område för alla matematiker. Primtal spelar även en stor roll i talteorin.
De första tjugo primtalen är (talföljd A000040 i OEIS):
Innehåll |
Hur avgör man om ett tal är ett primtal?
Om man vill avgöra om ett tal (p) är ett primtal, så ska man dividera det med alla som ligger mellan talet och 1. Men har man en lista över primtal räcker det med att dela med alla primtal mellan talet och 1, eftersom alla tal kan delas upp i primtal. Detta kan bli väldigt komplicerat om många divisioner behövs, men det finns en förenkling man kan använda sig av: Det man kan tänka på är att om p vore produkten av två mindre tal, så kan inte båda dessa vara större än kvadratroten av p; om så vore fallet skulle deras produkt vara större än talet p:
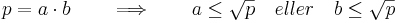 .
.
Exempel:
Är 103 ett primtal? Kvadratroten av 103 är cirka 10 (10,14889157...) varför det räcker med att testa om 103 är delbart med något primtal som är mindre än 10, det vill säga något av talen 2, 3, 5 eller 7. Talet 103 är udda och är därmed inte delbart med 2, och då dess siffersumma (1 + 0 + 3) inte är delbar med 3 är talet 103 inte delbart med 3 heller. Även delbarhet med talen 5 och 7 är uteslutna: 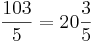 och
och 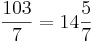 . Alltså är 103 ett primtal.
. Alltså är 103 ett primtal.
Denna metod är dock inte särskilt användbar i modern kryptografi, där man behöver primtal bestående av hundratals siffror; istället använder man sig av persondatorer som kan primtalstesta ett tal bestående av 100 siffror inom loppet av en sekund. Ett av många primtalstest är en algoritm kallad Eratosthenes såll: Denna algoritm plockar ut alla primtal upp till och med en vald övre gräns.
Det största kända primtalet
Oerhört mycket arbete har lagts ned på att försöka hitta allt större primtal. Det största primtal som hittills har hittats är 243 112 609 − 1. Utskrivet med siffror (i bas 10) är talet 12 978 189 siffror långt[1]. Primtalet hittades 23 augusti 2008 inom projektet GIMPS av matematikinstutionen på UCLA[2]
Det tidigare rekordet var 232 582 657 − 1, från den 4 september 2006 av Curtis Cooper och Steven Boone, som båda är professorer vid Central Missouri State University i USA. Detta tal, som är ett Mersenneprimtal, innehåller 9 808 358 siffror.
Det största kända primtalet, vars antal siffror självt är ett primtal, är 27 653 · 29 167 433 + 1 som har 2 759 677 siffror, utskrivet i bas 10.
Antalet primtal
Det finns oändligt många primtal, vilket bevisades av Euklides ca 300 f.Kr.
Bevis
Vi antar att det finns n stycken primtal och betecknar dem med symbolerna 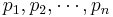 ; symbolen pk betecknar primtal nummer k. Av dessa bildar vi ett positivt heltal:
; symbolen pk betecknar primtal nummer k. Av dessa bildar vi ett positivt heltal:
Enligt Aritmetikens fundamentalsats kan detta tal skrivas som en produkt av våra primtal:
minst ett av de icke-negativa heltalen 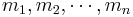 är större än noll. Säg att mk är större än noll. Då kan vi skriva
är större än noll. Säg att mk är större än noll. Då kan vi skriva 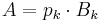 och
och 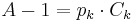 , där Bk och Ck är positiva heltal. Detta innebär att
, där Bk och Ck är positiva heltal. Detta innebär att 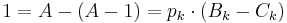 vilket endast är möjligt om pk = 1 och Bk − Ck = 1. Men pk är ett primtal och som sådant är det större än talet 1. Vi har därför fått motsägelsen att 1 > 1.
vilket endast är möjligt om pk = 1 och Bk − Ck = 1. Men pk är ett primtal och som sådant är det större än talet 1. Vi har därför fått motsägelsen att 1 > 1.
Slutsatsen är att det var fel av oss att anta att det fanns n stycken primtal. Detta innebär att antalet primtal är oändligt, vilket är vad vi ville bevisa.
Alternativt bevis
Leonhard Euler och Leopold Kroenecker visade år 1876 att antalet primtal är knutet till den harmoniska serien via följade samband:
där produkten beräknas över samtliga primtal, hur många de nu är; kom ihåg att vi ännu inte vet att det finns oändligt många av dem.
Det faktum att den harmoniska serien är divergent innebär att produkten också är divergent, vilket den endast kan vara om den består av oändligt många faktorer, vilket innebär att antalet primtal är oändligt många.
Sambandet som Euler och Kroenecker fann utgör startpunkten för det område inom matematik som kallas analytisk talteori; man använder resultat från matematisk analys för att studera problem inom talteori. Detta är en oväntad koppling, eftersom talteori sysslar med heltal (diskreta objekt) och matematisk analys med reella- och komplexa tal (icke-diskreta objekt).
Olösta problem
Det finns fortfarande många olösta gåtor angående primtalen:
- Finns det oändligt många primtalstvillingar?
- Finns det oändligt många primtal på formen n2+1?
- Finns det alltid ett primtal mellan n2 och (n + 1)2?
- Hur många primtal är fermattal? (Hittills har bara 5 hittats.)
- Innehåller Fibonaccitalföljden oändligt många primtal?
Tillämpningar
Under lång tid ansågs talteori i allmänet och studiet av primtal i synnerhet som det utmärkande exemplet på ren matematik, utan några tillämpningar utanför den egna teorin. Särskilt talteoretiker, som exempelvis G.H. Hardy, var stolta för att bedriva forskning som saknade betydelse för militären.[3] Hans visioner raserades när det offentliggjordes att primtal användes som byggstenar inom öppen-nyckel-kryptering.
Primtal används även för hashtabeller och pseudoslumptalsgeneratorer. En pseudoslumptalssekvens kan användas för utplacering av dubbar på ett dubbdäck för att undvika resonansfenomen.
Se även
- Tabell över primfaktorer
- Matematik
- Gaussiska primtal
- Mersenneprimtal
- Primtalssatsen
- Perfekt tal
- Relativt prima
- Primtalstvilling
- Aritmetikens fundamentalsats
- Ulams spiral
- Primorial
- Lista över primtal
Referenser
- ↑ Jan Melin (16 september 2008). ”Nytt primtalsrekord satt i dag”. Ny Teknik. http://www.nyteknik.se/nyheter/it_telekom/allmant/article412307.ece.
- ↑ http://mersenne.org/prime.htm , läst 17 september 2008
- ↑ Hardy, G.H. (1940). A Mathematician's Apology, Cambridge University Press. ISBN 0-521-42706-1. "No one has yet discovered any warlike purpose to be served by the theory of numbers or relativity, and it seems unlikely that anyone will do so for many years".
Litteratur
- Riesel, Hans, En bok om primtal, Lund 1968
Externa länkar
- http://mathworld.wolfram.com/topics/PrimeNumbers.html
- http://www2.math.su.se/matematik/exempel/tal/primtal.html
- Geometry of prime numbers and perfect numbers
- http://primes.utm.edu/
- Lista över stora möjliga primtal
- http://home.swipnet.se/ollevejde/matteord/primtal.htm
- http://www.utm.edu/research/primes/notes/proofs/infinite/.