Från Rilpedia

Två primtal är primtalstvillingar om differensen mellan dem är 2. Paret (2,3) är inte primtalstvillingar eftersom skillnaden mellan dessa är 1. Detta är även den minsta möjliga skillnaden mellan två primtal. De lägsta paret primtalstvillingar är därför 3 och 5.

Varje primtalstvilling som är större än 3 kan beräknas med hjälp av (6n − 1, 6n + 1), för något naturligt tal n. Talet n måste dock sluta på 0, 2, 3, 5, 7 eller 8 och får ej vara 1.

Största primtalstvillingar

Den 15 januari 2007 hittade Eric Vautier, (Frankrike), de hittills största primtalstvillingarna, 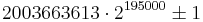. Talet har 58 711 siffror.

De första primtalstvillingarna (<884):

(3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193), (197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433), (461, 463), (521, 523), (569, 571), (599, 601), (617, 619), (641, 643), (659, 661), (809, 811), (821, 823), (827, 829), (857, 859), (881, 883)

Se även

• Talteori
• Matematik

Litteratur

Riesel, Hans, En bok om primtal, Lund 1968