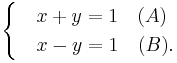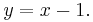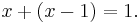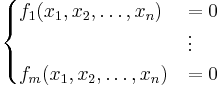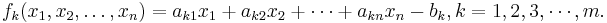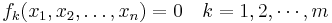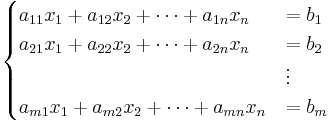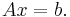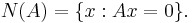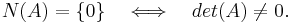Ekvationssystem

Från Rilpedia

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Ett ekvationssystem med två lösningar

Inom matematiken är ett ekvationssystem en samling av ekvationer. Varje ekvation beskriver en kurva, och lösningarna till ekvationssystemet är de punkter som ligger på samtliga kurvor.

Exempel

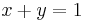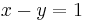Vi är intresserade av att bestämma de punkter som linjerna $x + y = 1\,$ och $x - y = 1 \,$ har gemensamt (deras skärningspunkter); med andra ord vill vi lösa ekvationssystemet

$\begin{cases} & x + y = 1 \quad (A)\\ & x - y = 1 \quad (B). \end{cases}$

Det första hindret som man skall övervinna är att reducera de två ekvationerna med de två obekanta talen ( $x$ och $y$ ) till endast en ekvation som innehåller ett obekant tal ( $x$ ). Vi gör detta genom att ta ekvation (B) och skriva om den så att talet $y$ står ensamt:

$y = x - 1.\,$

Sedan sätter vi in detta i ekvationen A på $y$ :s plats och får en ny ekvation som bara innehåller det okända talet $x$ :

$x + (x - 1) = 1.\,$

Denna ekvation har bara en lösning $x = 1.$ Vi vet att 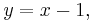$y = x-1,\,$ vilket innebär att om $x = 1$ så är $y = 0.$

Det finns därför bara en skärningspunkt, (x,y), mellan de två linjerna A och B: Den punkt vars x-koordinat är x=1 och vars y-koordinat är y=0.

Allmänna ekvationssystem

Säg att vi har m stycken funktioner, där varje funktion beror av n stycken variabler:

$f_1(x_1,x_2,\cdots,x_n) \quad \dots \quad f_m(x_1,x_2,\cdots,x_n).$

Varje ekvation

$f_k(x_1,x_2,\dots,x_n)=0$

beskriver en så kallad hyper-yta i det n-dimensionella Euklidiska rummet 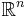$\mathbb{R}^n$ .

(Vi använder benämningen hyper-yta istället för benämningen yta eftersom ytor är två-dimensionella objekt, och hyper-ytor i 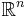$\mathbb{R}^n$ kan vara av dimensioner allt från 1 till n-1.)

Om det finns lösningar till ekvationssystemet

$\begin{cases} f_1(x_1,x_2,\dots,x_n)&=0\\ &\vdots\\ f_m(x_1,x_2,\dots,x_n)&=0 \end{cases}$

så är de punkter i det n-dimensionella rummet som ligger på samtliga m stycken hyper-ytor. (Systemet har endast lösningar om hyperytorna möts i minst en punkt.)

Innehåller ekvationssystemet färre ekvationer än variabler, det vill säga om m < n, så kallas det underbestämt. Då kan det fortfarande vara lösbart, men lösningen blir inte entydig. Lösningen kan till exempel vara alla tal på en kurva eller linje.

Innehåller det fler oberoende ekvationer än variabler, det vill säga om m > n, så kallas det överbestämt, och är oftast olösbart. Överbestämda ekvationssystem är vanliga inom forskningen, då man behandlar mätdata som innehåller slumpmässiga mätfel.

Linjära ekvationssystem

Den enklaste formen av ekvationssystem får man om samtliga funktioner är linjära:

$f_k(x_1,x_2,\dots,x_n) = a_{k1} x_1 + a_{k2} x_2 + \cdots + a_{kn} x_n - b_k, k=1,2,3,\cdots,m.$

Var och en av de m stycken ekvationerna

$f_k(x_1,x_2,\dots,x_n) = 0 \quad k=1,2,\cdots,m$

beskriver ett så kallat hyper-plan i det n-dimensionella rummet:

$a_{k1} x_1 + a_{k2} x_2 + \cdots + a_{kn} x_n = b_k.$

Det linjära ekvationssystemet

$\begin{cases} a_{11} x_1 + a_{12} x_2 + \cdots + a_{1n} x_n &= b_1\\ a_{21} x_1 + a_{22} x_2 + \cdots + a_{2n} x_n &= b_2\\ &\vdots\\ a_{m1} x_1 + a_{m2} x_2 + \cdots + a_{mn} x_n &= b_m \end{cases}$

beskriver skärningspunkterna mellan de m hyper-planen.

En förutsättning för att det skall finnas en unik lösning till ekvationssystemet är att det finns lika många (icke-parallella) hyper-plan som det finns variabler i ekvationerna, det vill säga att m = n.

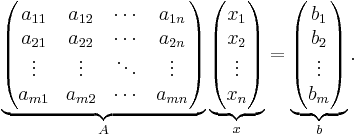
Ekvationssystemet kan skrivas med hjälp av matriser på följande sätt:

$\underbrace{\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix}}_A \underbrace{\begin{pmatrix} x_1\\x_2\\ \vdots\\x_n \end{pmatrix}}_x = \underbrace{\begin{pmatrix} b_1\\b_2\\ \vdots\\b_m \end{pmatrix}}_b.$

Ett mer kortfattat sätt att skriva detta väldiga uttryck på är

$Ax = b.\,$

Om A är en inverterbar matris med inversen 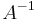$A^{-1}\,$ , så kan lösningen till ekvationssystemet skrivas

$x = A^{-1}\,b$ .

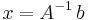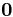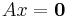För att detta skall vara möjligt måste matrisen A vara kvadratisk, det vill säga den måste ha lika många rader (m) som kolumner (n), och dessutom får dess nollrum, N(A), bara innehålla noll-vektorn $\mathbf{0}$ ; Nollrummet till matrisen A består av de vektorer som är lösningar till ekvationssystemet $Ax=\mathbf{0}$ :

$N(A) = \{x : Ax = 0\}.\,$

Nollrummet N(A) innehåller endast noll-vektorn om, och endast om, determinanten till matrisen A inte är noll:

$N(A) = \{0\} \quad \Longleftrightarrow \quad det(A) \neq 0.$

Vi använder symbolerna det(A) för att beteckna det tal som är determinanten av matrisen A.

Sammanfattningsvis kan vi konstatera att:

Varje kvadratisk matris, A, kan associeras med ett speciellt tal, det(A). Det linjära ekvationssystemet Ax = b har en unik lösning om, och endast om, detta tal inte är noll.

Referenser

J. Peterson, Tillämpad linjär algebra, (1993), Jan Peterson
L. Råde och B.Westergren, BETA: mathematics handbook, (1990), Studentlitteratur
P.R. Halmos, Finite-dimensional vector spaces, (1987), Springer-Verlag

Ekvationssystem

Från Rilpedia

Innehåll

Exempel

Allmänna ekvationssystem

Linjära ekvationssystem

Referenser

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk