Addition

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
3+2=5 med äpplen, ett vanligt val i skolböcker.

Addition är ett av de grundläggande fyra räknesätten (operatorerna) inom aritmetiken. Den grundläggande binära operationen betecknas oftast med plustecknet, + (Unicode-kod U+0025). Upprepad addition betecknas med summatecken 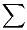\sum\,, ursprungligen den versala grekiska bokstaven Σ, sigma.


Vid addition läggs värdet av två (eller flera) tal, termer, ihop till en summa, till exempel 1 + 2 = 3. För att lägga ihop n tal behövs n −1 additioner av två tal. Addition av ett negativt tal är ekvivalent med subtraktion.

Samma namn och beteckningar används också i andra situationer för att beteckna binära operationer med likartade egenskaper; se exempelvis vektoraddition.

Att summan av sex och två är 8 skrivs: 6+2=8 Och utläses: "sex adderat med två är åtta" eller "sex plus två är åtta"

Addition betecknas med tecknet plus (+). Tecknet + infördes omkring år 1500. a+b uttrycker att a och b är adderade till en summa, summan är resultatet av additionen. Summan av två naturliga tal a och b kan uppfattas som antalet objekt i den uppsättning som ges av att till en uppsättning med a objekt foga en uppsättning med b objekt. Addition av tal lyder under en kompositionsregel; två element ställs samman och resulterar i ett element. a och b ställs samman och bildar exempelvis c. Vid addition av talet 0 till ett element a bibehålls a oförändrat, a+0=a. Noll förändrar inte a’s värde vid addition, detta gäller för varje tal a. [1]


Innehåll

Additionslagar

Plustecknet.

Lagarna gäller för alla tal a,b och c.

a+0=a

a+(b+c)=(a+b)+c kallas för den associativa lagen

a+b=b+a kallas för den kommutativa lagen

Additionen är även transitiv[2], om a=b så är a+c=b+c


Den associativa och kommutativa lagen medför att en kontroll av summan kan göras genom att summera termerna i en annan ordning. [3]

Ett exempel på detta är följande summa:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45

som blir enklare att summera om ordningen på termerna kastas om:

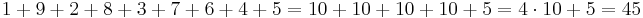
1+9+2+8+3+7+6+4+5=10+10+10+10+5=4 \cdot 10+5=45

I den andra uträkningen användes multiplikation, ett sätt att snabbt summera ett visst antal termer av samma värde; a+a+a+a=4a.


Addition av algebraiska uttryck

Vid addition av algebraiska uttryck adderas termer av samma slag var för sig genom att deras koefficienter adderas. Exemplet (2x2 + 3x + 1) + (3x2 + x + 4) = 5x2 + 4x + 5 visar hur addition av algebraiska termer går till.


Addition av komplexa tal

Ett komplext tal brukar skrivas a+bi a + bi där a och b är reella tal och i är imaginärt i satisfieras av i2 = − 1. I uttrycket a + bi kallas a för realdelen och b för imaginärdelen.[4]

(a + bi) + (c + di) = (a + c) + (b + d)i

Vid addition av komplexa tal adderas således realdel och imaginärdel var för sig.


Addition av vektorer

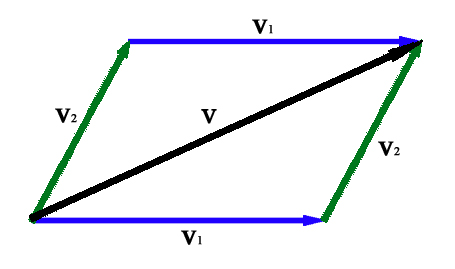
Följande defineringar av addition av vektorer gäller för godtycklig dimension, för enkelhetens skull visas här addition av vektorer i planet.

Låt v1 och v2 vara två riktade sträckor med samma utgångspunkt. Deras summa, eller resultant som det kallas för vektorer, består i den riktade diagonal i det parallellogram som spänns upp av v1 och v2. Denna sträcka har samma utgångspunkt som v1 och v2. Detta sätt att summera vektorer på går under parallellogramlagen.[5] Vektor v1 och vektor v2 kallas för komposanter, de bygger upp resultanten v.

I figuren nedan adderas vektor v1 (blå) och vektor v2 (grön) och bildar resultantvektorn v (svart). Detta illustreras genom att den blå vektorn läggs ut först och vid dess spets startar den gröna vektorn, den svarta vektorn har sin startpunkt i den blå vektorns stjärt och sin slutpunkt vid den gröna vektorns spets. Om v2 och v1 adderas istället så börjar man med den gröna vektorn först och lägger sedan på den blå. Som synes i figuren skapar de blå och gröna vektorerna ett parallellogram vars diagonal utgörs av den resulterande vektorn.

Addition av vektorer 003.jpg

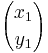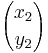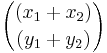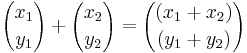Om v1 och v2 representeras av två talpar {x_1 \choose y_1} och {x_2 \choose y_2} blir deras summa den vektor som representeras av {(x_1+x_2)\choose (y_1+y_2)}, det vill säga {x_1 \choose y_1}+{x_2 \choose y_2}={(x_1+x_2)\choose (y_1+y_2)}.

Addition av vinklar

Vid addition av riktade vinklar räknas moturs positivt och medurs negativt. Summan av A+B är således den rotation som ges av att först utföra rotationen A och därefter rotationen B. En rotation först på 60° och därefter 30° blir en total rotation på 90° som visas genom följande uträkning 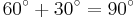60^\circ+30^\circ=90^\circ. Timvisaren på en klocka visar 12.00, efter 3 timmar har visaren rört sig -90°, efter 13 timmar har visaren rört sig -360°+(-30°)=-390°. Efter 1 timme och 13 timmar är vinkeln mellan 12:an på klockan och timvisaren densamma, 30°.[6]


Addition av bråktal

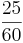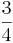För att addera bråktal krävs det att bråktalen har samma nämnare. Om \frac{25}{60} och \frac{3}{4} ska adderas söks den minsta gemensamma nämnaren, MGN. För att lösa addition av bråktal räcker det dock med att hitta en gemensam nämnare och överföra de olika bråktalen till denna nämnare. I detta fall är till exempel 12 en gemensam nämnare, men även 60 och 240 är gemensamma nämnare. Detta problem kan illustreras i att räkna ut den totala tiden 25 minuter plus 3/4 timme. 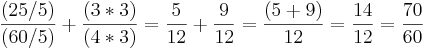\frac{(25/5)}{(60/5)}+\frac{(3*3)}{(4*3)}=\frac{5}{12}+\frac{9}{12}=\frac{(5+9)}{12}=\frac{14}{12}=\frac{70}{60}, svaret blir således att den totala tiden är 70 minuter.

Allmänt gäller: 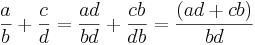\frac{a}{b}+\frac{c}{d}=\frac{ad}{bd}+\frac{cb}{db}=\frac{(ad+cb)}{bd} om b och d är skilda från noll.


Trigonometriska additionsformler

Nedan följer de vanligast trigonometriska additionsformlerna som används när till exempel vinklar adderas eller subtraheras från varandra.[7]

sin(A + B) = sinAcosB + cosAsinB

sin(A − B) = sinAcosB − cosAsinB

cos(A + B) = cosAcosB − sinAsinB

cos(A − B) = cosAcosB + sinAsinB


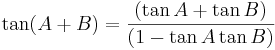
\tan (A+B)=\frac{(\tan A + \tan B)}{(1-\tan A \tan B)}


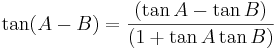
\tan (A-B)=\frac{(\tan A - \tan B)}{(1+\tan A \tan B)}


Addition av transfinita tal

Ett transfinit tal är ett oändligt ordinaltal eller ett oändligt kardinaltal. Skillnaden på ordinaltal och kardinaltal är att i ordinaltalet spelar platsen i mängden roll. Ett oändligt kardinaltal uttrycker ”storleken” av en oändlig mängd. Två mängder säges ha samma kardinaltal eller mäktighet om de på ett en-entydigt sätt kan ordnas till varandra.[8]

För oändliga kardinaltal m gäller följande aritmetik:


m + 1 = m

m + m = m


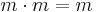
m \cdot m=m

Källor

  1. ↑ William Karush: Matematisk uppslagsbok översatt och bearbetad av Jan Thompson och Bertil Rahm, 1962. ISBN 91-46-13004-7. 
  2. ↑ Bo Göran Johansson: Matematikens historia, 2004. ISBN 91-44-03322-2. 
  3. ↑ William Karush: Matematisk uppslagsbok översatt och bearbetad av Jan Thompson och Bertil Rahm, 1962. ISBN 91-46-13004-7. 
  4. ↑ William Karush: Matematisk uppslagsbok översatt och bearbetad av Jan Thompson och Bertil Rahm, 1962. ISBN 91-46-13004-7. 
  5. ↑ William Karush: Matematisk uppslagsbok översatt och bearbetad av Jan Thompson och Bertil Rahm, 1962. ISBN 91-46-13004-7. 
  6. ↑ William Karush: Matematisk uppslagsbok översatt och bearbetad av Jan Thompson och Bertil Rahm, 1962. ISBN 91-46-13004-7. 
  7. ↑ Jan Thompson & Thomas Martinsson: Matematiklexikon, 1991. ISBN 91-46-16515-0. 
  8. ↑ William Karush: Matematisk uppslagsbok översatt och bearbetad av Jan Thompson och Bertil Rahm, 1962. ISBN 91-46-13004-7. 

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Addition"
Personliga verktyg