Från Rilpedia
Texten från svenska Wikipedia
Platonska kroppar är konvexa tredimensionella geometriska kroppar (polyedrar) med likformiga polygoner som sidor. I varje hörn möts lika många sidor. Euklides bevisade att det bara finns 5 stycken sådana kroppar.
Inom alkemin antogs dessa kroppar motsvara de klassiska elementen.
| Kropp |
Sidor |
Antal hörn |
Antal kanter |
| Tetraeder |
4 liksidiga trianglar |
4 |
6 |
|
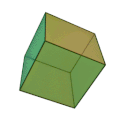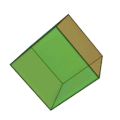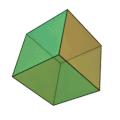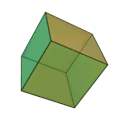
| Kub (hexaeder) |
6 liksidiga kvadrater |
8 |
12 |
|
| Oktaeder |
8 liksidiga trianglar |
6 |
12 |
|
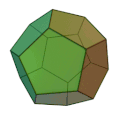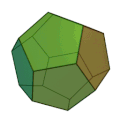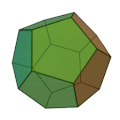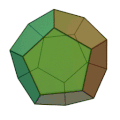
| Dodekaeder |
12 regelbundna pentagoner |
20 |
30 |
|
| Ikosaeder |
20 liksidiga trianglar |
12 |
30 |
|
Om man frångår kravet på konvexitet, d.v.s. tillåter att kroppen även har inbuktningar, stiger antalet möjliga kroppar till det oändliga, även om sidoytorna ska vara liksidiga och likadana. Till exempel kan man ersätta varje yta i ikosaedern med en tetraeder och få en taggig stjärnform med 60 sidor, eller koppla ihop valfritt antal dodekaedrar på olika sätt. Men då är det inte längre fråga om Platonska kroppar.
Platons kroppar är de polyedrar som är de mest rättvisa
tärningarna, på grund av sina regelbundna former
Se även
