Vektoranalys

Från Rilpedia

Texten från svenska Wikipedia

Vektoranalys är ett område i matematiken som handlar om reell analys i flera variabler av vektorer i 2 eller fler dimensioner. Den absoluta majoriteten av användningsområdena baserar sig på 3-dimensionell vektoranalys.

Vektoranalysen består av ett antal formler och problemlösningstekniker som är mycket användbara för ingenjörer och fysiker.

Vi betraktar vektorfält, vilka åt varje punkt i rummet tilldelar en vektor, och skalärfält, vilka åt varje punkt i rummet tilldelar en skalär. Till exempel så är temperaturen i en pool ett skalärfält: för varje punkt i poolen finns en temperatur (vilket anges som ett reellt tal). Hur vattnet strömmar i poolen är däremot ett vektorfält: i varje punkt kan vi mäta vattnets hastighet, med riktning, d.v.s. en hastighetsvektor.

Tre viktiga operatorer inom vektoranalysen:

gradient: mäter hastighet och riktning av ett förändringar i ett skalärfält; gradienten av ett skalärfält är ett vektorfält.
rotation:mäter ett vektorfälts tendens att rotera runt en punkt; rotationen av ett vektorfält är ett annat vektorfält.
divergens: mäter ett vektorfälts tendens till att utgå ifrån eller närma sig en given punkt; divergensen av ett vektorfält är ett skalärt fält.

Exempel

Gradienten av temperaturfältet ovan ger en vektor i varje punkt, som hela tiden pekar mot varmare vatten (högre temperatur). Om skalärfältet betecknas med T, så skrivs gradienten av T som grad T eller ∇ T
Rotationen av vattnets hastighetsvektor ovan anger, löst talat, om det finns virvlar i vattnet. Ett vektorfält v har rotationen rot v, eller ∇× v
Divergensen av vattnets hastighetsvektor anger, löst talat, huruvida det i en punkt tillkommer mer vatten (divergensen positiv) eller strömmar ut vatten (divergensen negativ). Om v åter är hastighetsvektorn, så är divergensen ∇·v

Flertalet analytiska resultat förstås lättare om man använder sig av tekniker från differentialgeometrin, vilken innehåller hela vektoranalysen plus lite extra: exempelvis hur man generaliserar vektoranalysen till högre dimensioner. Att det inte går att göra likadant i högre dimensioner som man gör i 3, beror bl.a. på att det inte går att på ett naturligt sätt generalisera rotationsoperatorn.

Definitioner

Följande definitioner gäller i ett kartesiskt koordinatsystem $\{\bar{e_0}, \ldots, \bar{e_n}\}$ , där basvektorerna är konstanta.

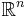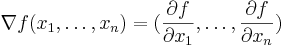Låt f vara ett skalärfält definierat i en delmängd av $\mathbb{R}^n$ . Gradienten av $f$ definieras då som $\nabla f(x_1, \ldots, x_n) =( \frac{\partial f}{\partial x_1}, \ldots, \frac{\partial f}{\partial x_n})$ .
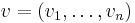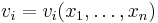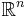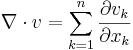Låt $v=(v_1,\ldots,v_n)$ vara en vektor, och varje $v_i=v_i(x_1, \ldots , x_n)$ är en funktion definierad i en given delmängd av $\mathbb{R}^n$ . Divergensen av $v$ definieras då som: $\nabla \cdot v = \sum_{k=1} ^n \frac{\partial v_k}{\partial x_k}$ .
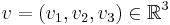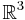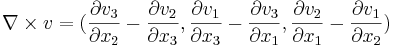Låt $v = (v_1,v_2,v_3)\in \mathbb{R}^3$ , och varje $v i (x 1, x 2, x 3)$ vara en funktion definierad i en given delmängd av $\mathbb{R}^3$ . Rotationen av $v$ definieras då som: $\nabla \times v=(\frac{\partial v_3}{\partial x_2}-\frac{\partial v_2}{\partial x_3},\frac{\partial v_1}{\partial x_3}-\frac{\partial v_3}{\partial x_1},\frac{\partial v_2}{\partial x_1}-\frac{\partial v_1}{\partial x_2})$ .