Gradient

Från Rilpedia

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Två typer av gradienter, cirkulär och linjär.

Gradient är inom matematiken en vektorvärd funktion av ett skalärfält som i kartesiska koordinater är

$\ \, \nabla f = \mathrm{grad} \, f = \left(\frac{\partial f}{\partial x} , \frac{\partial f}{\partial y} , \frac{\partial f}{\partial z}\right)$

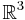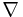för $\mathbb{R}^3$ , där $\nabla$ är nablaoperatorn, som även kan användas för andra typer av operationer inom vektoranalysen.

Mer generellt kan gradienten skrivas som en funktional: $\nabla: D_{\mathbb R^N \rightarrow \mathbb R} \rightarrow D_{\mathbb R^N \rightarrow \mathbb R^N}$

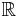där $D_{\mathbb R^N \rightarrow \mathbb R}$ betecknar mängden av alla differentierbara funktioner från $\mathbb R^N$ till $\mathbb R$ osv.

Gradienten $\nabla f$ av en funktion $f$ är sedan en vektor som pekar i den riktning som $f$ lutar brantast i och med storlek proportionerlig mot lutningen hos $f$ .

Exempel

Tag funktionen $f(x,\,y) = \sin(2x)\cos(y)$ . Uttryckt i kartesiska koordinater har denna gradient $grad\,f = \nabla f = \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right)^T = (2\cos(2x)\cos(y), -\sin(2x)\sin(y))^T$ . Om vi till exempel tittar i punkten $(x,\, y) = (0.4,\, -0.7)$ blir gradienten $\nabla\, f = (1.4,\, -0.25)$ .