Stokes sats

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Stokes sats, efter George Gabriel Stokes, säger att för varje kontinuerligt deriverbar funktion gäller, då C=δS är en sluten kurva i rummet, följande:

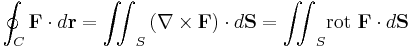
  1. \oint_{C}{\mathbf{F}\cdot d\mathbf{r}}={\iint}_S\left(\nabla\times\mathbf{F}\right)\cdot d\mathbf{S}={\iint}_S\mbox{rot }\mathbf{F}\cdot d\mathbf{S}
    eller
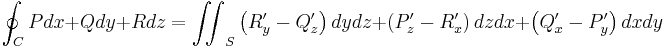
    \oint_{C}{P}dx+{Q}dy+{R}dz={\iint}_S\left(R_y'-Q_z'\right)dydz+\left(P_z'-R_x'\right)dzdx+ \left(Q_x'-P_y'\right)dxdy
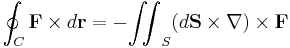
  2. \oint_{C}{\mathbf{F}\times d\mathbf{r}}=-{\iint}_{S}{\left(d\mathbf{S}\times\nabla\right)\times\mathbf{F}}
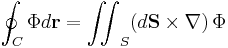
  3. \oint_{C}{\Phi d\mathbf{r}}={\iint}_{S}{\left(d\mathbf{S}\times\nabla\right)\Phi}

I differentialgeometri använder man sig av en formalism som tillåter de ovanstående likheterna att skrivas som en enda likhet

∫ ω = ∫ dω
C S

där ω är en differentialform, och d är den yttre differentialen, och alla integraler är tagna lämpligt antal gånger. Den stora vitsen med detta uttryck är att det omedelbart generaliserar till högre dimensioner, då är S ett n-dimensionellt område och C är dess rand. Likväl så gäller samma formel i en dimension om man med integralen över ett 0-dimensionell mängd syftar på funktionsevaluering och tänker på att randen av ett intervall är två punkter. Detta specialfall är den välkända analysens fundamentalsats. Ett annat specialfall är Greens sats.

Hämtad från "https://sv.rilpedia.org/wiki/Stokes_sats"
Personliga verktyg