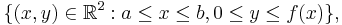Integral
Från Rilpedia
Integral inom integrationteorin är ett matematiskt begrepp som används för att ange "storleken" på en funktion. Integraler används för att beskriva och beräkna geometriska och fysikaliska storheter som längd, area, massa, volym och flöde, där den kan beskrivas som en summa av en variabel. Integrering är beräkningen av en integral. Integrationteori är ett mycket viktigt område inom matematisk analys och sannolikhetsteori med väntevärder.
Integrationteorin hör samman med måtteorin eftersom man studerar storleken. Därför hör integrationteorins historia i många stycken samman med måtteoris historia. Pionjärerna inom integrationteorin är Isaac Newton, Gottfried Leibniz, Bernhard Riemann, Henri Lebesgue och Percy Daniell. Isaac Newton och Gottfried Leibniz identifierade integral med intuitiv kalkyl, integralkalkyl, som sambanden integralen med derivatan. Bernard Riemann konstruerad mer exakt integralen, Riemannintegralen, för funktioner i 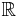 . Henri Lebesgue utvecklade den revolutionär Lebesgueintegralen som användar måtteori. Percy Daniell definierad en generell integral, Daniellintegralen, som inte behöver måtteoretiska begrepp.
. Henri Lebesgue utvecklade den revolutionär Lebesgueintegralen som användar måtteori. Percy Daniell definierad en generell integral, Daniellintegralen, som inte behöver måtteoretiska begrepp.
Innehåll |
Bakgrund
Informellt kan vi inte "mäta" funktioner utan informationen från funktionens invärden och utvärden. Därför vill man definiera integralen med hjälp av funktionens invärden och utvärden. Till exempel låt ![f : [-1,1] \rightarrow \R](/w/images/sv.rilpedia.org/math/1/0/5/105fdf393ff64f4184d3ad75d0f61e51.png) är en funktion definierad som:
är en funktion definierad som:
Hur kan vi mäta "storleken" på funktionen f? Funktionen f är definierad i [-1,1] så man kunde säga att storleken för funktionen f är måttet för [-1,1] dvs talet 2. Men nu använder vi bara informationen från funktionens invärden:
Vi använder ingen informationen från utvärdet:
Å andra sidan kunde man använda bara utvärden och sedan mäta utvärdenas mått som är 1. Men liksom ovan använder vi nu ingen information från invärden.
Integralen är en begrepp som använder ömse information. Å andra sidan hur vi använder den här informationen är en svår fråga och där finns många svar: Riemannintegralen, Lebesgueintegralen, Daniellintegralen, Kurvintegralen, Riemann-Stieltjes integralen och så vidare.
Med intuitiviteten kan man säga att om ![f : [a,b] \rightarrow \R](/w/images/sv.rilpedia.org/math/c/b/f/cbf6bcd3aa5cc7cdf73d8d1c12387715.png) var
var 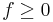 så är integralen mellan a och b ett "mått" på mängden
så är integralen mellan a och b ett "mått" på mängden
dvs arean under 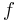 :s funktionskurvan.
:s funktionskurvan.
Riemannintegral
Riemanns idé var att man kunde definiera integralen för begränsad funktioner i  med "kolonn-approximationen". Först fördelar man invärden till intervall och utväljer en punkt från alla intervall. Sedan har man en kolonn vars mått man kan mäta. Riemann-summa är en summa av de här kolonners mått. De här Riemannsummor approximerar funktionens arean under en funktionskurva och därför definierar man Riemannintegralen så att det är de gränsvärden för Riemannsummor.
med "kolonn-approximationen". Först fördelar man invärden till intervall och utväljer en punkt från alla intervall. Sedan har man en kolonn vars mått man kan mäta. Riemann-summa är en summa av de här kolonners mått. De här Riemannsummor approximerar funktionens arean under en funktionskurva och därför definierar man Riemannintegralen så att det är de gränsvärden för Riemannsummor.
Lebesgueintegral
Riemannintegralens svagheten är att det ses inte mängden som är fraktal karaktär. Man kan fixa det med måtteorin. Först vi definierar integralen för karakteristisk funktioner eftersom deras storkheten är invärders måttet. Sedan vi definierar integralen för enkel funktioner som är summan av karakteristisk funktioner. Eftersom man kan approksimera mätbara funktioner med karakteristisk funktioner, till slut man kan definiera integralen för alla mätbara funktioner.
Den här metoden kallas Lebesgueintegration och integralen kallas måttintegral. Lebesgueintegralen är en måttintegral vars måttet är Lebesguemåttet
Daniellintegral
Lebesgueintegralens svagheten är att man behöver måtteori. Daniellintegralen är en integral som behöver ingen måtteori. Först man definiera en klass av funktioner kallas testfunktioner. Här man definiera att testfunktioner är begränsad funktioner så att summan av testfunktioner är en testfunktion och testfunktions absolutbelopp är också ett testfunktion.
Sedan man definiera en funktional, elementarintegralen, över testfunktionfamiljen så att det är linjär, kontinuerlig och ingen negativ operator. Om vi kan approksimera en funktion med testfunktioner man definierar Daniellintegralen för den funktionen så att det är den gränsvärden av elementarintegraler av testfunktioner.
Integralkalkyl
Integralkalkyl är benämningen på själva uträkningen av specifika integraler. För enklare integraler kan detta ofta göras direkt med hjälp av resultaten från analysens huvudsats, medan mer komplicerade fall kan kräva partiell integrering eller Fourieranalys.
Integrerbarhet
Med varje integraler det är inte alltid naturligt att definiera integralen för alla funktioner. Med till exempel Lebesgueintegralen och Riemannintegralen där finns många funktioner som är inte resonlig att integrera. Följaktligen, man måste betrakta en mindre klass av funktioner, integrerbar funktioner, som är naturligt att integrera. Där finns många definitioner för integrerbarhet och beror på vilken integralen man användar.
Se även
Externa länkar
- The Integrator - Beräknar primitiva funktioner





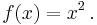
![\mbox{dom}(f) = [-1,1]\, .](/w/images/sv.rilpedia.org/math/7/b/a/7bab6441bc10e3045f5f5082b528a24c.png)
![\mbox{im}(f) = [0,1]\, .](/w/images/sv.rilpedia.org/math/2/2/f/22f14d2e20372d73a48ba79bed91ec11.png)