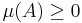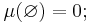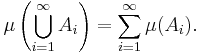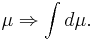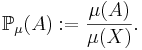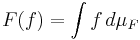Mått (matematik)

Från Rilpedia

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Informellt avbildar ett mått en mängd på ett positivt reellt tal, där delmängder avbildas till mindre tal.

Mått inom måtteorin är ett matematiskt begrepp som används för att ange "storleken" på en mängd. Längd, area och volym är några exempel på vanliga mått. Begreppet är centralt för att på ett korrekt sätt kunna definiera integralen av en funktion på ett generellt sätt. Måtteori är ett mycket viktigt område inom matematisk analys och sannolikhetsteori.

Idéer för måtteori fanns i det antika Grekland, då Arkimedes ville fastställa det exakta värdet på cirkelns område. Men måtteori är en 1900-talsuppfinning. Pionjärerna inom måtteori är Henri Lebesgue, Georg Cantor, Émile Borel, Constantin Carathéodory och Alfred Haar. Henri Lebesgue utvecklade det revolutionerande Lebesguemåttet och Lebesgueintegralen i 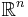$\R^n$ . Georg Cantor och Émile Borel identifierade senare mätbara mängder och Borelmängder. Constantin Carathéodory definierade yttre mått och Carathéodorys konstruktion. Alfred Haar är känd för Haarmåttet, ett koncept som liknar Lebesguemåttet i topologiska grupper.

Bakgrund

Har alla föremål en volym?

Huvudartikel: Mätbara mängder.

Volymen av en kub kan definieras som höjden gånger bredden gånger djupet. Med hjälp av geometrin kan en volym tilldelas till sfärer, pyramider och andra former. Men går det att tilldela en volym till alla föremål i tre dimensioner? En sådan funktion, Volym(x) måste (minst) ha följande egenskaper:

Om x och y är två ej överlappande föremål så är

Volym(x och y) = Volym(x) + Volym(y)
Ett föremål som roteras och förflyttas behåller samma volym.
Volymen av ingenting är 0.
Volymen är alltid större än eller lika med 0, men kan vara oändlig.
Volymen av en 1x1x1-kub är 1.

Tyvärr visar det sig att det är omöjligt att hitta en definition på volym som uppfyller dessa krav. Kraven är logiskt självmotsägande. Lösningen blir att kalla vissa föremål för mätbara och vissa, mycket konstiga, föremål för icke mätbara och nöja sig med att kunna tilldela en volym till de mätbara föremålen.

Om det första kravet skärps till att även gälla uppräkneligt många kombinationer av föremål (vilket nästan alltid görs i matematiken) går det heller inte att definiera yta och längd i 2 respektive 1 dimension. Detta är bakgrunden till måtteorin, den gren av matematiken som specificerar hur längd, yta och volym kan mätas för godtyckliga föremål på ett tillfredsställande sätt.

Banach-Tarskis paradox

Huvudartikel: Banach-Tarskis paradox.

Ett klot kan faktiskt med bara fem bitar pusslas ihop till två stycken klot identiska med det första!

Banach och Tarski visade i en artikel publicerad 1924 följande resultat, av många betraktat som mycket förvånande:

För alla två tredimensionella föremål A och B går det att dela upp A i ett visst antal (n stycken) bitar och genom att rotera och flytta dessa bitar bilda B (utan hål).

Satsen säger till exempel att en ärta kan delas i ändligt många bitar som kan pusslas ihop till ett (solitt) jordklot. Detta brukar kallas Banach-Tarskis paradox. Lösningen ligger i att "bitarna" kommer att vara så väldigt komplicerade att det inte går att definiera deras volym på ett vettigt sätt. Bitarna har bland annat den exotiska egenskapen att deras volym förändras när de roteras.

Konstruktion av mått

Huvudartikel: Yttre mått.

Istället för att släppa på något av kraven ovan, brukar problemet lösas genom att ett mått bara definieras på en samling mätbara mängder. Det visar sig att denna samlig kan göras mycket stor, innefattandes i stort sett alla mängder som matematiker kommer i kontakt med.

Själva konstruktionen går till genom att måttet defineras för vissa enkla mängder, med vilka alla mängder kan täckas över. Ett exempel är alla intervall $(a, b)$ som kan få måttet $b - a$ . Måttet för en övertäckning är summan av alla enkla mängder som ingår i övertäcknignen. En godtycklig mängd kan övertäckas på många olika sätt; måttet för mängden är måttet för den minsta möjliga övertäckningen. Mer formellt kallas detta ett yttre mått, som definieras för alla delmängder. Detta uppfyller inte alla krav för ett mått. Med hjälp av det yttre måttet kan mätbarhet definieras och man kan visa att det yttre måttet i själva verket är ett mått för dessa mätbara mängder.

Formell definition

Ett mått, 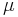$\mu\,$ , är formellt en funktion definierad på en σ-algebra 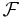$\mathcal{F}$ över en mängd 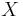$X\,$ med värdemängd i $[0,\infty]$ (se utökade reella tallinjen) som uppfyller följande:

Icke-negativitet: ingen mängd har negativt mått:

$\mu(A) \geq 0$

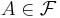för alla $A \in \mathcal{F}$ ;

Tomma mängden har måttet noll:

$\mu(\varnothing) = 0;$

Uppräkneligt additivitet eller σ-additivitet: om 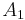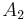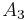$A_1\,$ , $A_2\,$ , $A_3\,$ , ... är en uppräknelig följd av parvis disjunkta mängder i 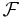$\mathcal{F}$ , så gäller

$\mu\left(\bigcup_{i=1}^\infty A_i\right) = \sum_{i=1}^\infty \mu(A_i).$

Medlemmarna i 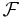$\mathcal{F}$ kallas mätbara mängder och trippeln 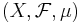$(X,\mathcal{F},\mu)$ kallas måttrum.

Egenskaper

Huvudartikel: Egenskaper hos mått.

Flera egenskaper kan härledas från definitionen på uppräkneligt additivt mått. Bland annat flera satser med gränsvärden av mått som visar sig användbara vid definitionen av Lebesgueintegralen.

Typer

Där finns många typer av mått:

Mängdteoretiska mått; de här mått användar bara mängders egenskaper:

Ett mått är ett fullständigt mått om varje delmängd av en nollmängd är mätbar.
Ett mått är ett bildmått om man det är en bild av andra måttet i mätbara avbildningen.
Ett mått är ett produktmått om det är en produkt av andra mått.

Topologiska mått; de här mått behöver också topologiska strukturen i måttrummet:

Ett mått är ett Borelmått om varje Borelmängd är mätbar.
Ett Borelmått är ett Radonmått om vi kan approximera Borelmängder med kompakta och öppna mängder.

Algebraiska mått; de här mått användar algebraiska konstruktionen:

Ett Radonmått är ett Haarmått om det är volyminvariant, dvs om vi draga mängder måttet ändras inte.
Ett Radonmått är ett tangentmått om det approksimerar andra måttet i en punkt såsom tangenter approksimerar funktioner.

Metriska mått; de här mått användar metriska stukturen:

Ett Borelmått är ett Carlesonmått om vi kan mäta en intuitiv volym för rander.
Ett Radonmått är ett Ahlfors-regelbundet mått om vi kan mäta bollen såsom Lebesguemått.

Exempel

Det finns många klassiska konstruktioner för mått. Följande mått är ofta använda inom måtteorin.

Enkla mått

Huvudartiklar: Diracmått och Räknemått

Det finns några triviala mängdfunktioner som är mått.

Diracmåttet är det enklast tänkbara måttet. Det koncentrerar alla massa i en enda punkt. Å andra sidan är Diracmåttet viktigt inom funktionalanalys, specifikt distributionsteorin.

Räknemåttet, som är en summa av Diracmått, är ett enkelt mått som är lika med antalet element för mängden. Detta måttet har också applikationer i serieteori.

Längd, area och volym

Huvudartiklar: Lebesguemått och Hausdorffmått

Den väsentliga motivationen för nämnet mått är att mäta intuitiva längder areor eller volymer för mängder. Det finns några klassiska mått som gör just det.

Lebesguemåttet är det första måttet i måtteori som motsvarar den allmänna uppfattningen om vad längd, area och volym innebär. Det är definierat i 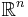$\R^n$ med hjälp av geometriska måttet för rätblock. Det är också en måtteoretisk utvidgning för Jordanmåttet, som trots sitt namn inte är ett mått.

Hausdorffmåttet är ett modernare mått än Lebesguemåttet. Hausdorffmåttet kan även mäta längd, area och volym för mångfalder, vilket inte Lebesguemåttet kan. Dessutom är det med Hausdorffmåttet möjligt att definiera Hausdorffdimensionen, som är viktig inom fraktalgeometri. Därför grundar sig hela geometriska måtteorin på Hausdorffmåttet. Hausdorffmåttet är definierad i generella metriska rum.

Speciella mått

Huvudartiklar: Vridningsinvariant mått, Grassmannmått och Favardmått

Det också finns många speciella mått som inte nödvändigtvis kan tolkas som en längd, area eller volym.

Vridningsinvariant mått är Haarmått i ortogonalgrupper som bevarar vridningar. Eftersom ortogonalgrupper är matrisgrupper så mäter vridningsinvarianta mått "matrismängder".

Grassmannmåttet, som är ett bildmått av ett vridningsinvariant mått, mäter "delrummängder" i Grassmannmångfalder. Det är också "rotations"invariant eftersom vridningsinvariant mått är Haarmått.

Favardmåttet är definierad med hjälp av måttintegralen med avseende på Grassmannmåttet. Det är ett viktigt mått för rektifierbara mängder.

Mätbarhet

Huvudartiklar: Mätbarhet och Konstruktion av en icke mätbar mängd.

Det är inte självklart vilken sigma-algebra man väljer för måttrummet. Till exempel med Diracmåttet och räknemåttet det är naturligt att man välja alla mängder som mätbara mängder. Å andra sidan finns det för de flesta mått, till exempel Lebesguemåttet, icke mätbara mängder, som är inte möjliga att mäta på ett rimligt sätt. Därför måste man analysera mätbarheten för mängder, dvs vilken mängder som är möjliga att mäta.

Existensen av mängder i euklidiskt rum som inte går att mäta med Lebesguemåttet (längd, area, volym) beror helt på om man accepterar urvalsaxiomet eller inte. Alla bevis som visar på en existens av en icke mätbar mängd måste använda sig av detta. Idag använder sig alla matematiker av detta axiom, så gott som utan undantag. Urvalsaxiomet säger att givet en stor samling mängder går det att välja exakt ett element ur var och en av dessa mängder. Det kan tyckas trivialt, men om samlingen är mycket stor får det icke-triviala följder som nämnts ovan.

Integration

Huvudartikel: Lebesgueintegration.

Med måttstrukturen kan man definiera storleken för mängden. Å andra sidan man kan också analysera "storleken" på mätbara funktionen med hjälp av måttstrukturen, eftersom måttet alltid definierar en integral med Lebesgues definition. Den här integralen, som kallas måttintegralen, är viktig eftersom alla mått definierar en måttintegralen, dvs för måttet

$\mu \Rightarrow \int d\mu.$

Tillämpningar

Det finns många tillämpningar av måtteori inom matematik.

Geometrisk måtteori är viktig inom teoretiska fraktalgeometri.

Geometri

Huvudartikel: Geometrisk måtteori

Abram Samoilovitch Besicovitch och Herbert Federer definierade geometrisk måtteori för undersökning av geometrisk struktur av mängder och mått med måtteori. Nuförtiden, geometrisk måtteori undersöker begrepp som är antingen fraktal- eller slätt karäktar. Den mest viktiga mått som man användar här är Hausdorffmåttet.

Man undersöker begrepp med fraktal karäktar med hjälp av en fraktaldimension, Hausdorffdimension, vilken säger mer om en rad fina strukturer av mängder än exempelvis en traditionell dimension. Det är definierad med hjälp av Hausdorffmåttet. Dessutom man undersöker begrepp med slätt karäktär med hjälp av en begrepp rektifierbarhet. Den är en koncept som generaliserar differentialgeometriska begrepp mångfalder och differentialformer så att de här nästan överallt "slätt". Så att man definierar rektifierbar mängder och rektifierbar strömer. De är också definierade med hjälp av Hausdorffmåttet.

Sannolikhet

Huvudartikel: Sannolikhetsteori

Måtteori revolutionerade sannolikhetsberäkning. Andrej Kolmogorov utvecklade axiom för sannolikhet. Han definierade sannolikhetsrumet så att sannolikhet som ett mått och händelser som en sigma-algebra. Idag kallas sannolikhetsräknande med teoretiska aspekter sannolikhetsteori.

Sannolikhetsteori är huvudsakligen samma teori än måtteori med ändligt mått eftersom varje ändligt mått är efter normering ett sannolikhetsmått. Mer precist, om 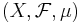$(X,\mathcal{F},\mu)$ är ett måttrum där måttet är ändligt, dvs 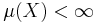$\mu(X) < \infty$ , kan man definiera ett sannolikhetsmått $\mathbb{P}_\mu : \mathcal{F} \longrightarrow [0,1]$ ,

$\mathbb{P}_\mu (A) := \frac{\mu(A)}{\mu(X)}.$

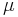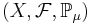Det geometriska sannolikhetsrummet för måttet $\mu\,$ är en trippel $(X,\mathcal{F},\mathbb{P}_\mu)$ .

Funktionalanalys

Huvudartikel: Funktionalanalys

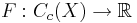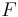Radonmått är ganska liknande med linjär funktionaler. Med Riesz-Markovs satsen kan man karakterisera varje Radonmått med måttintegraler. Mer precist, om $F : C_c(X) \rightarrow \R$ är en positiv linjär funktional om och endast om det finns ett Radonmått $\mu_F : \mbox{Bor}\,X \rightarrow [0,\infty]\,$ så att man kan representera varje $F\,$ med hjälp av Radonmåttet 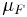$\mu_F\,$ . Detta innebär

$F(f) = \int f \, d\mu_F$

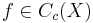för alla $f \in C_c(X)\,$ .

Därför kallas man ofta positiva linjära funktionaler Radonmått inom funktionalanalys. Så att också positiva linjära funktionaler har alla naturliga egenskaper hos mått likså sigma-additivitet, subadditivitet, monotonicitet och konvergenssatser.

Se även

Måtteori

Mått (matematik); Konstruktion av en icke mätbar mängd
Definition: Yttre mått; Egenskaper hos mått
Begrepp: Nollmängd; Nästan överallt; Fullständigt mått
Integration: Mätbar funktion; Lebesgueintegration; Egenskaper hos måttintegral

Referenser

H. Lebesgue, Intégrale, longueur, aire, Université de Paris, 1902
P. Halmos, Measure theory, D. van Nostrand and Co., 1950
M. E. Munroe, Introduction to Measure and Integration, Addison Wesley, 1953
H. Federer, Geometric measure theory, Springer-Verlag, 1969
R. M. Dudley, Real Analysis and Probability, Cambridge University Press, 2002
G. B. Folland, Real Analysis: Modern Techniques and Their Applications, John Wiley and Sons 1999 ISBN 0-471-317160-0
A. Friedman, Foundations of Modern Analysis, Dover Publications, 1982
D. H. Fremlin, Measure Theory, Torres Fremlin, 2000; tillgänglig online på http://www.essex.ac.uk/maths/staff/fremlin/mt.htm