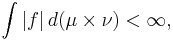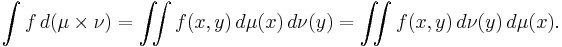Produktmått
Från Rilpedia
Produktmått är inom matematiken ett typ av mått som är en produkt av andra mått.
Innehåll |
Produkt sigma-algebra
Låt  ,
,  , vara en familj av mätbara rum. Indexmängden
, vara en familj av mätbara rum. Indexmängden 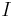 kan vara en godtycklig mängd - även ouppräknelig. Låt X vara en cartesisk produkt av mängderna
kan vara en godtycklig mängd - även ouppräknelig. Låt X vara en cartesisk produkt av mängderna 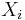 , dvs
, dvs
En mängd 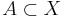 är en kon om det finns en ändlig mängd
är en kon om det finns en ändlig mängd 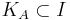 och mängder
och mängder 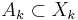 ,
, 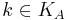 , så att
, så att
Med andra ord, konen är en produkt:
där
dvs bara ett ändlig antal av 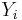 är icke-
är icke-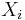 .
.
En kon  är en mätbar kon om
är en mätbar kon om
för alla 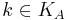 .
.
Låt 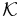 vara en familj av alla mätbara koner.
vara en familj av alla mätbara koner.
En produkt sigma-algebra, 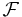 , är en sigma-algebra genererad av alla mätbara koner. Mer precist, en produkt sigma-algebra är
, är en sigma-algebra genererad av alla mätbara koner. Mer precist, en produkt sigma-algebra är
Detta innebär att produkt sigma-algebran är den minsta av de sigma-algebror som har alla mätbara koner som en del av sig.
När 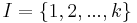 är en ändlig mängd betecknas ofta produkt sigma-algebran
är en ändlig mängd betecknas ofta produkt sigma-algebran
Produktmått
Man definierar produktmåttet med hjälp av mätbara koner.
Låt 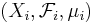 ,
, 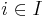 , vara en familj av sigma-ändliga måttrum. Man behöver sigma-ändlighet här eftersom produktmåttet inte är unikt med icke-sigma-ändliga måttrum.
, vara en familj av sigma-ändliga måttrum. Man behöver sigma-ändlighet här eftersom produktmåttet inte är unikt med icke-sigma-ändliga måttrum.
För en kon
definiera ett "mått"
Den här funktionen ![\tau : \mathcal{K} \rightarrow [0,\infty]\,](/w/images/sv.rilpedia.org/math/9/1/0/910db8446ddd6290e45bacb38e1fa5dc.png) är sigma-additiv och
är sigma-additiv och 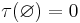 . Tyvärr är det inte ett mått eftersom mätbara koner
. Tyvärr är det inte ett mått eftersom mätbara koner 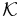 inte bildar en sigma-algebra.
inte bildar en sigma-algebra.
Å andra sidan det går att visa att 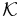 bildar en algebra, dvs
bildar en algebra, dvs
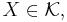
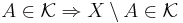 och
och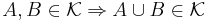 .
.
Dessutom är produkt sigma-algebran genererad av en algebra 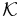 . Därför, med Carathéodorys utvidgningsats, innebär detta att det finns en unik utvidgning,
. Därför, med Carathéodorys utvidgningsats, innebär detta att det finns en unik utvidgning, ![\mu : \mathcal{F} \rightarrow [0,\infty]\,](/w/images/sv.rilpedia.org/math/a/e/6/ae6f627ce2b2a61aa53a4fd65310ceeb.png) , för funktionen
, för funktionen 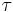 som är ett mått, som kallas produktmåttet. Det är ofta betecknat
som är ett mått, som kallas produktmåttet. Det är ofta betecknat
så att en trippel
är ett måttrum.
När 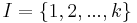 är en ändlig mängd går det ofta att beteckna produktmåttet
är en ändlig mängd går det ofta att beteckna produktmåttet
Exempel
Lebesguemåttet i  , när
, när 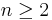 , är inte ett produktmått. Intuitionen sägar att
, är inte ett produktmått. Intuitionen sägar att
men det är inte så för alla Lebesguemätbara mängder. Till exempel låt 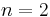 och
och 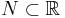 vara en icke Lebesguemätbar mängd. Så att mängden
vara en icke Lebesguemätbar mängd. Så att mängden
är 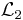 -mätbar eftersom
-mätbar eftersom
 .
.
Å andra sidan det är icke  -mätbar eftersom
-mätbar eftersom
![A \notin [\mbox{Leb}\,\R] \otimes [\mbox{Leb}\,\R]](/w/images/sv.rilpedia.org/math/0/9/c/09cc157e419a1d16ed89a64d5a90c322.png) .
.
Så att
Å andra sidan är Lebesguemåttet produktmåttet när man bara använder Borelmängder. Det går att visa att
och för alla ![[\mbox{Bor}\,\R]](/w/images/sv.rilpedia.org/math/1/9/c/19c674d9cdbae7d686b204a7880f5260.png) -mätbara koner
-mätbara koner 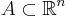
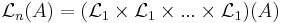 .
.
Så att
eftersom produktmåttet är en unik utvidgning.
Fubinis sats
En viktig tillämpning för produktmåttet är Fubinis sats. Det sägar att man kan ändra integrerordningen. Låt 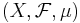 och
och 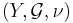 vara sigma-ändliga måttrum och
vara sigma-ändliga måttrum och 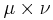 vara produktmåttet.
vara produktmåttet.
Fubinis sats säger att om 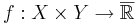 är integrerbar med avseende på produktmåttet
är integrerbar med avseende på produktmåttet 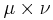 , dvs
, dvs
så är
Se även
Referenser
- P. Halmos, Measure theory, D. van Nostrand and Co., 1950.




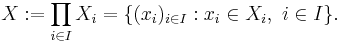
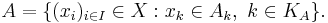
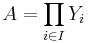
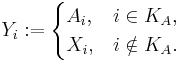
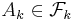
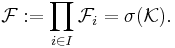

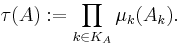
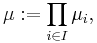
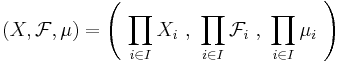

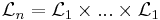

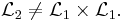
![\mbox{Bor}\,\R^n = [\mbox{Bor}\,\R] \otimes [\mbox{Bor}\,\R] \otimes ... \otimes [\mbox{Bor}\,\R] ,](/w/images/sv.rilpedia.org/math/a/0/7/a071a8d26016e019ae4a41ff5cba8aa0.png)
![\mathcal{L}_n | \mbox{Bor}\,\R^n = [\mathcal{L}_1 | \mbox{Bor}\,\R] \times [\mathcal{L}_1 | \mbox{Bor}\,\R] \times ... \times [\mathcal{L}_1 | \mbox{Bor}\,\R],](/w/images/sv.rilpedia.org/math/c/d/d/cddf070ccc7ac84678abf5d9c34bc60e.png)