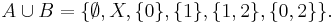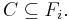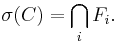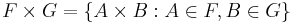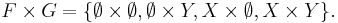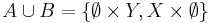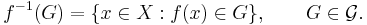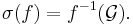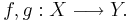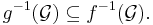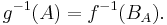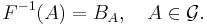Sigma-algebra
Från Rilpedia
En σ-algebra (sigma-algebra) är ett matematiskt objekt
som är av central betydelse då man studerar måtteori och integrationsteori.
Syftet med begreppet sigma-algebra är att beskriva vilka delar av en given mängd X som går att mäta. En ofta använd strategi att lösa problem eller lära sig om hur ett föremål är beskaffat är att splittra upp det i mindre beståndsdelar för att därefter studera dessa separat. Nu kan man inte splittra upp ett objekt i vilka delar som helst, utan dessa måste se ut på ett visst sätt. Den matematiska motsvarigheten till det sätt på vilket ett objekt får splittras i är begreppet sigma-algebra. Genom att utesluta vissa, "mycket konstiga", delmängder av X får man en sigma-algebra som är mycket lättare att hantera.
Innehåll |
Formell beskrivning
En σ-algebra (sigma-algebra) över en mängd X är en familj 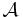 av delmängder av X som är sådan att
av delmängder av X som är sådan att
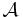 är icke-tom:
är icke-tom: 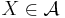
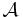 är sluten under komplementsbildning:
är sluten under komplementsbildning: 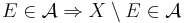 .
.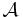 är sluten under uppräkneliga unioner. Det innebär att om mängderna
är sluten under uppräkneliga unioner. Det innebär att om mängderna  tillhör
tillhör 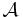 , så är deras union
, så är deras union 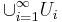 också ett element i
också ett element i 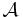 .
.
Om 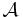 är en sigma-algebra i X så man kallas ofta paret
är en sigma-algebra i X så man kallas ofta paret 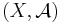 ett mätbart rum.
ett mätbart rum.
En viktig detalj att notera är att elementen i en sigma-algebra på X utgörs av delmängder till X, inte punkter i X.
- Om vi exempelvis låter X vara två-punkts mängden X = { 0, 1 }, så kan en sigma-algebra på X vara familjen { Ø, X }; I denna sigma-algebra är mängden X ett element.
Ett sätt att visualisera detta är följande.
- Låt X vara en LEGOTM-modell och delmängder till X vara bitar av modellen. En sigma-algebra på X kan då uppfattas som en påse (mängd) som innehåller modellen och dess bitar.
Snitt och unioner av sigma-algebror
Låt A och B vara två sigma-algebror på mängden X.
- Snittet
 är också en sigma-algebra på X. Den är en del-sigma-algebra av både A och B.
är också en sigma-algebra på X. Den är en del-sigma-algebra av både A och B. - Unionen
 är inte nödvändigtvis en sigma-algebra på X.
är inte nödvändigtvis en sigma-algebra på X.
Följande exempel visar att familjen  inte behöver vara en sigma-algebra, bara för att familjerna A och B är det.
inte behöver vara en sigma-algebra, bara för att familjerna A och B är det.
- Tag mängden X = {0,1,2} och de två sigma-algebrorna A = { Ø, X, {0}, {1,2} } samt B = { Ø, X, {1}, {0,2} }. Unionen av dessa sigma-algebror är familjen
- Om detta vore en sigma-algebra så skulle unionen, {0,1}, av mängderna {0} och {1} vara ett element i familjen
 .
.
Sigma-algebra genererad av familj av delmängder
Låt C vara en godtycklig familj av delmängder till en mängd X. Det finns sigma-algebror, Fi, av olika storlekar som har familjen C som en del av sig:
Den minsta av dessa sigma-algebror kallas sigma-algebran genererad av familjen C och betecknas σ(C); den är definierad som snittet av alla sigma-algebror som omfattar C:
Exempel: Borel sigma-algebra
Ett exempel på en sigma-algebra som är genererad av en familj av delmängder ges av ett topologiskt rum (X,T): Objektet T är en familj av delmängder till X som besitter vissa egenskaper; för detaljer se artikeln Topologiskt rum. Sigma-algebran, σ(T), genererad av denna familj kallas Borel sigma-algebran på X.
Exempel: Produkt sigma-algebra
Låt (X,F) och (Y,G) vara två mätbara rum. På den cartesiska produkten 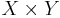 skall en sigma-algebra konstrueras baserad på de tillgängliga sigma-algebrorna F och G.
skall en sigma-algebra konstrueras baserad på de tillgängliga sigma-algebrorna F och G.
- En första tanke kanske är att bilda familjen M bestående av alla produkter
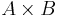 , där A är ett element i F och B ett element i G:
, där A är ett element i F och B ett element i G:
- Denna familj behöver inte vara en sigma-algebra på
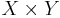 bara för att F är en sigma-algebra på X och G är en sigma-algebra på Y, vilket följande exempel visar.
bara för att F är en sigma-algebra på X och G är en sigma-algebra på Y, vilket följande exempel visar.
-
- Låt F = { Ø, X } vara den triviala sigma-algebran på X och G = { Ø, Y } den triviala sigma-algebran på Y. Produkten av dessa familjer är familjen
-
- Om vi tar de två elementen
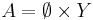 och
och 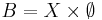 , så måste deras union
, så måste deras union
- vara ett element i familjen om denna är en sigma-algebra på den cartesiska produkten
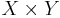 .
.
- Om vi tar de två elementen
Den korrekta definitionen av produkt-σ-algebran på 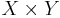 är som den minsta sigma-algebra som innehåller familjen
är som den minsta sigma-algebra som innehåller familjen 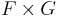 ovan; den vanligast förekommande beteckningen för denna är
ovan; den vanligast förekommande beteckningen för denna är 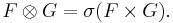
Sigma-algebra genererad av en avbildning
Låt 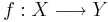 vara en avbildning från det mätbara rummet
vara en avbildning från det mätbara rummet 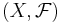 till det mätbara rummet
till det mätbara rummet 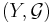 . Detta innebär att familjen
. Detta innebär att familjen 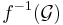 är en delfamilj av sigma-algebran
är en delfamilj av sigma-algebran 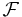 . Elementen i denna familj ser ut på följande sätt:
. Elementen i denna familj ser ut på följande sätt:
De utgör en sigma-algebra på mängden X – faktum är att detta är den minsta sigma-algebra på X som gör f till en mätbar avbildning.
Man kallar den för sigma-algebran genererad av avbildningen f och skriver σ(f):
Sigma-algebra genererad av flera avbildningar
Låt 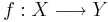 och
och 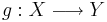 vara två avbildningar från det mätbara rummet
vara två avbildningar från det mätbara rummet 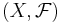 till det mätbara rummet
till det mätbara rummet 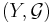 .
.
Unionen  av det två sigma-algebrorna
av det två sigma-algebrorna 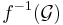 och
och 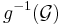 är inte nödvändigtvis själv en sigma-algebra på X; det är däremot sigma-algebran
är inte nödvändigtvis själv en sigma-algebra på X; det är däremot sigma-algebran
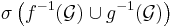 .
.
Detta är den minsta sigma-algebra på X som gör både f och g till mätbara avbildningar. Man kallar detta för sigma-algebran genererad av avbildningarna f och g, och skriver
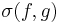 .
.
På samma sätt som ovan definierar man sigma-algebran 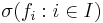 genererad av avbildningar
genererad av avbildningar 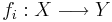 från det mätbara rummet
från det mätbara rummet 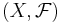 till det mätbara rummet
till det mätbara rummet 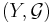 .
.
Doob-Dynkins lemma
Låt f och g vara två avbildningar från det mätbara rummet 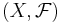 till det mätbara rummet
till det mätbara rummet 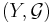 :
:
Avbildningen g är mätbar med avseende på sigma-algebran genererad av f om, och endast om, det finns en mätbar avbildning F som "sammanbinder" avbildningarna f och g:
Skrivet på "matematiska":
Bevis av Doob-Dynkins lemma
Antag att avbildningen g är mätbar med avseende på sigma-algebran genererad av avbildningen f:
Varje element 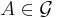 motsvaras då av ett element
motsvaras då av ett element 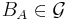 som är sådant att
som är sådant att
Denna association definierar en mätbar avbildning, 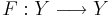 på mängden Y:
på mängden Y:
Denna avbildning "sammanbinder" de två avbildningarna f och g: