Uppräknelig
Från Rilpedia
En mängd är uppräknelig om den har samma kardinaltal som en delmängd till de naturliga talen, det vill säga ett ändligt tal eller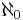 
. Exempel: Mängderna {1, 2, 3, 4, 5, 6, 7} och {A, B, C, D, E, F, G} är båda uppräkneliga med kardinaltalet 7 i båda fallen.
Alla naturliga tal är var för sig uppräkneliga. Ett tal n vilket som helst har ju kardinaliteten n eftersom |n| = n (se artikeln mängd). Men hela mängden av naturliga tal, N, är också uppräknelig, men oändlig, eftersom den är en delmängd till sig själv.
Kardinaltalet för en uppräkneligt oändlig mängd är Alef-noll (Alef-0, 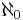), som också är den "minsta" oändligheten. Exempel på uppräkneligt oändliga mängder: naturliga tal, hela tal och rationella tal. En oändlig mängd som ej är uppräknelig kallas överuppräknelig (eller ouppräknelig).
Beteckningen "uppräknelig" kommer av att alla mängder med denna egenskap i princip kan räknas upp. De naturliga talen kan ju räknas upp enligt den vanliga metoden 1, 2, 3, 4 etc. I praktiken kommer vi aldrig hinna räkna upp alla, men vi hinner fram till varje element inom ändlig tid. De rationella talen kan räknas upp genom att skriva dem på bråkform i särskilt kvadratiskliknande schema där man ser att det finns en sick-sack-väg genom schemat med vilken man får med alla talen.
På liknande sätt som man kan visa att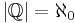 
, kan man visa en uppräknelig union av uppräkneliga mängder är uppräknelig.
Exempel
Man kan visa att mängden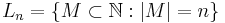 
är uppräknelig för alla n. Därför är 
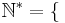alla ändliga delmängder av 
= 
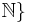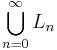uppräknelig. Notera att 
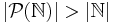, så att motsvarande påstående för mängden av alla delmängder av 
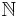, potensmängden av 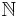, inte gäller.
Se även
