Kontinuumhypotesen

Från Rilpedia

Texten från svenska Wikipedia

Kontinuumhypotesen är ett mängdteoretiskt påstående som bland annat har betydelse inom matematikfilosofin. Hypotesen är att det inte existerar något kardinaltal som ligger mellan kardinaltalet för mängden av de hela talen, Alef-noll, och kardinaltalet för mängden av de reella talen, kontinuum.

Kurt Gödel bevisade med hjälp av det konstruktibla universat att antagandet att kontinuumhypotesen är sann inte strider mot mängdlärans axiom i systemet ZFC. Emellertid visade matematikern Paul Cohen genom att introducera metoden forcing år 1963 att inte heller antagandet att kontinuumhypotesen är falsk strider mot axiomen i ZFC. Det är alltså likgiltigt för mängdläran huruvida ett sådant kardinaltal existerar eller inte, man kan inte avgöra med dess hjälp huruvida det finns eller inte.

Att kontinuumhypotesen är oavgörbar innebär, enligt dem som förespråkar matematisk realism, att axiomsystemet ZFC inte beskriver den matematiska verkligheten tillräckligt precist för att kontinuumhypotesens verkliga sanningsvärde skall kunna avgöras. Andra realister hävdar att det kan existera parallella mängdteoretiska universa: vissa där kontinuumhypotesen är sann och andra där den är falsk. Om man är formalist tolkar man i stället resultatet bara som en matematisk egenskap hos ZFC som formellt system.

Ett fåtal nutida mängdteoretiker, framförallt Hugh Woodin, anser att en djupare förståelse av mängdläran kan leda till insikter som får oss att acceptera nya axiom som skulle kunna avgöra kontinuumhypotesen. Bland sådana är tendensen numera snarare att tro att kontinuumhypotesen är falsk än att den är sann.

Generaliserade kontinuumhypotesen

Den generaliserade kontinuumhypotesen säger att 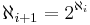$\alef_{i+1} = 2 ^ {\alef_i}$ , för alla oändliga kardinaltal 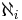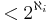$\alef_i$ . $<2 ^{ \alef_{i}}$ ska här förstås som kardinaliteten av potensmängden av en mängd med kardinalitet 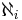$\alef_{i}$ . Kontinuumhypotesen blir då ett specialfall som säger att 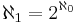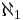$\alef_1 = 2 ^ {\alef_0}$ . $\alef_1$ är det kardinaltal som är närmast större än 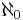$\alef_0$ . Liksom kontinuumhypotesen är generaliserade kontinuumhypotesen oavgörbar. Närmare bestämt kan man visa (Eastons sats) att de enda bevisbara egenskaperna för exponentfunktionen på sk. reguljära kardinaltal är monotonicitet och Königs sats.