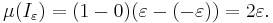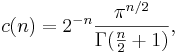Lebesguemått
Från Rilpedia
Lebesguemått är inom matematik ett begrepp som mätar till exempel längd, yta och volym för mängder i en, två och tre dimensioner. Lebesguemåttet är den först icke-triviallt mått inom måtteori. Det är definierad i euklidiska rummet 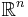 .
.
Lebesguemåttet var definierad i 1902 i artikel [1]. Det är namngett efter Henri Lebesgue som uppfann det.
Innehåll |
Yttre Lebesguemått
Likså ofta inom måtteori Lebesguemåttet är formellt först definierad med hjälp av ett yttre mått kallas Lebesgue yttre mått. Med yttre mått man kan mäta alla mängder men det är nödvändigtvis inte ett mått.
n-intervall
Lebesgues idé var att använda den linjära strukturen i 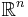 så att det är lätt att beräkna måttet för mängder. Man täcker mängden som ska mätas med rätblock eftersom volymen då är lätt att beräkna och sen vi tar den minsta summavolymen av rätblocken. Ett "rätblock" i flera dimensioner kallas n-intervall och volymen n-måttet.
så att det är lätt att beräkna måttet för mängder. Man täcker mängden som ska mätas med rätblock eftersom volymen då är lätt att beräkna och sen vi tar den minsta summavolymen av rätblocken. Ett "rätblock" i flera dimensioner kallas n-intervall och volymen n-måttet.
Mer exakt, en mängd 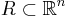 är ett n-intervall, om det finns
är ett n-intervall, om det finns 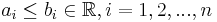 så att
så att
Där 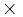 innebär cartesisk produkt.
innebär cartesisk produkt.
I geometri definieras ofta längden för intervallet ![[a,b]\,](/w/images/sv.rilpedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png) att vara talet
att vara talet 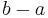 . Därför kan man definiera det n-måttet för ett n-intervall
. Därför kan man definiera det n-måttet för ett n-intervall 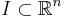 så att det är talet
så att det är talet
Nu är det möjligt att mäta storleken på alla n-intervall i 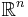 . Man kan använda detta för att mäta storleken av alla mängder i
. Man kan använda detta för att mäta storleken av alla mängder i 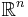 .
.
Så att man har nu definierad "måttet" för alla n-intervall.
Alla mängder
Nästa graden är utvidga den här definitionen för alla mängder.
Låt 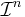 vara familjen av alla n-intervall i
vara familjen av alla n-intervall i 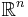 .
.
Det yttre Lebesguemåttet är en funktion ![\mathcal{L}_n^* : \mathcal{P}(\R^n) \rightarrow [0,+\infty]](/w/images/sv.rilpedia.org/math/1/0/e/10ef96d6a3e5f56b2c7b70569d912e36.png) , definierad som:
, definierad som:
Så att "måttet" är nu definierat för alla mängder i 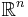 .
.
Man kallas den här funktionen yttre Lebesguemåttet eftersom det är ett yttre mått. Mer precist funktionen 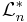 uppfyller följande kriterier:
uppfyller följande kriterier:
- Icke-negativitet: ingen mängd har negativt yttre Lebesguemått:
-
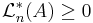 ,
,
- för alla
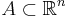 .
.
- Tomma mängden har måttet noll:
-
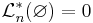 ,
,
- Monotonicitet: om
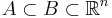 , så är
, så är
- Subadditivitet: om
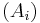 är en uppräknelig följd av mängder i
är en uppräknelig följd av mängder i 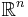 så är
så är
-
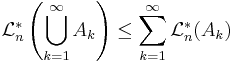 .
.
Lebesguemått
Yttre Lebesguemått är inte ett mått eftersom det är inte sigma-additiv. Så att det finns för mycket mängder att mäta. Därför man måste identifiera vilken mängder är inte resonliga att mäta.
Man säger att 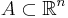 är en Lebesguemätbar mängd om det uppfyller Carathéodorys kriterium: för all
är en Lebesguemätbar mängd om det uppfyller Carathéodorys kriterium: för all 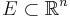 :
:
Det går att visa att där finns mängder som inte är icke Lebesguemätbara. Om man begränsa yttre Lebesguemåttet till Lebesguemätbara mängder det är ett mått.
Mer precist, låt 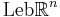 vara familjen av alla
vara familjen av alla 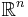 Lebesguemätbara mängder.
Lebesguemätbara mängder.
Eftersom funktionen 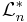 är ett yttre mått, man kan visa att familjen
är ett yttre mått, man kan visa att familjen 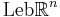 är en sigma-algebra och att funktionen
är en sigma-algebra och att funktionen 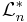 är uppräkneligt additiv för alla Lebesguemätbara mängder. Därför är funktionen
är uppräkneligt additiv för alla Lebesguemätbara mängder. Därför är funktionen
ett mått, kallat n-dimensionella Lebesguemåttet.
Innre Lebesguemått
Carathéodorys kriterium för Lebesguemätbarhet är ganska abstrakt definitionen och inte nödvändigtvis den mest intuitiva. För mängder med ändliga yttre Lebesguemåttet det finns andra definitionen för mätbarhet som är ekvivalent med Carathéodorys kriteriumen. Den här är definierad med hjälp av innre Lebesguemåttet.
Till exempel om ![A \subset [0,1]](/w/images/sv.rilpedia.org/math/e/a/3/ea35b5aa91d2767abfc101aed07adc6b.png) är Lebesguemätbar så är måttet för
är Lebesguemätbar så är måttet för 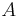 talet
talet ![1 - \mathcal{L}_1^* ([0,1] \setminus A)](/w/images/sv.rilpedia.org/math/c/1/1/c11cb20c38617f2f131e362d089cdaa4.png) . Lickså om
. Lickså om ![A \subset [0,1]^n](/w/images/sv.rilpedia.org/math/7/b/4/7b432654a90259fb5a6c2fcdd81633df.png) är Lebesguemätbar så är måttet för
är Lebesguemätbar så är måttet för 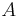 talet
talet ![1 - \mathcal{L}_1^* ([0,1]^n \setminus A)](/w/images/sv.rilpedia.org/math/c/c/1/cc10da97602f8f374200603d2a6656ee.png) . Innre Lebesguemåttet utvidgas den här begrepp för hela rummet
. Innre Lebesguemåttet utvidgas den här begrepp för hela rummet 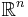 .
.
För 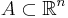 med
med 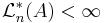 det innre Lebesguemåttet är talet
det innre Lebesguemåttet är talet
Det går att visa att för 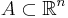 med
med 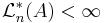
 .
.
Den koppling till yttre Lebesguemåttet är att för 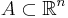 med
med 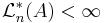
- är
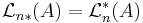
- mängden
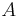 är Lebesguemätbara.
är Lebesguemätbara.
Exempel
- Låt
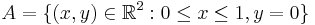 , och för alla
, och för alla 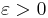 låt
låt ![I_\varepsilon := [0,1]\times[-\varepsilon,\varepsilon].](/w/images/sv.rilpedia.org/math/8/1/c/81ce9868063cc91d8062113d7261f6e2.png)
Det följer att 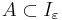 :s 2-mått är
:s 2-mått är
Så att
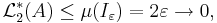 när
när 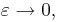
följaktligen är 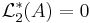 eftersom
eftersom 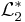 inte är negativ.
inte är negativ.
- Alla uppräkneliga mängder är nollmängder. Låt
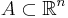 vara en uppräknelig mängd. Då
vara en uppräknelig mängd. Då
Eftersom 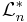 är subadditiv så är
är subadditiv så är
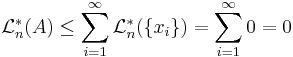 ,
,
dvs 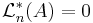 .
.
- Det finns även överuppräkneliga mängder som har Lebesguemåttet noll, exempelvis har Cantormängden 1-dimensionella Lebesguemåttet noll.
- Det går även att visa att om
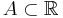 och varje delmängd till A är Lebesguemätbar så är
och varje delmängd till A är Lebesguemätbar så är 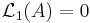 . En följd av detta är att varje mängd som har positivt mått har en delmängd som inte är mätbar.
. En följd av detta är att varje mängd som har positivt mått har en delmängd som inte är mätbar.
Egenskaper
Lebesguemåttet är ett ganska naturligt mått i 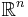 . Yttre Lebesguemåttet är ett yttre regelbundet och metriskt yttre mått
. Yttre Lebesguemåttet är ett yttre regelbundet och metriskt yttre mått
och Lebesguemåttet är ett Borelmått, ett Radonmått, ett Haarmått, ett komplett mått och ett Ahlfors-regelbundet mått i 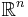 . Det är även ett produktmått över Borelmängder.
. Det är även ett produktmått över Borelmängder.
Tyvärr, Lebesguemåttet är inte bra att mäta mängder med "för mycket" geometriska strukturen, likså mångfalder och fraktaler. För det här det finns ett mer modernt mått, Hausdorffmåttet, som gör just det.
Å andra sidan i 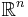 finns det ett
finns det ett 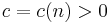 så att
så att
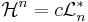 ,
,
där 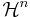 är n-dimensionella yttre Hausdorffmåttet och
är n-dimensionella yttre Hausdorffmåttet och
där 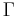 är Gammafunktionen.
är Gammafunktionen.
Se även
Källor
- Bourbaki, N. (2004), Integration I, Springer-Verlag
Referenser
- ↑ Henri Lebesgue (1902). "Intégrale, longueur, aire". Université de Paris.


![R = [a_1,b_1]\times [a_2,b_2] \times ... \times [a_n,b_n].](/w/images/sv.rilpedia.org/math/9/1/7/91713b77be583ab60113aff08c472a25.png)
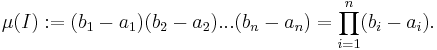
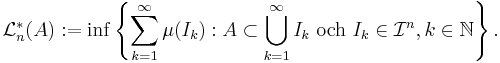
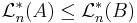
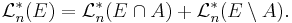
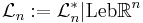
![\mathcal{L}_{n*} (A) := \limsup_{k \rightarrow \infty} \, \left[ \mathcal{L}_n^* ([-k,k]^n) - \mathcal{L}_n^* ([-k,k]^n \setminus A) \right] .](/w/images/sv.rilpedia.org/math/d/0/c/d0ccf63ce9ad591450c9169f9ceb59aa.png)