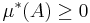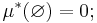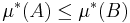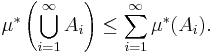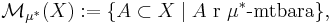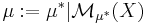Yttre mått

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Yttre mått är ett begrepp i måtteori som används som hjälp till att definiera mått.

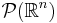Det går inte att definiera ett mått i \R^n så att alla mängder är mätbara (se mått). Genom att ställa lite mindre krav på måttet får man istället ett yttre mått som uppfyller liknande men svagare krav än för mått. Genom att studera det yttre måttet kan man identifiera en delmängd av \mathcal{P}(\R^n) som man kallar mätbara mängder. Slutligen kan man visa att det yttre måttet begräsat till de mätbara mängderna i själva verket är ett mått.

Innehåll

Formell definition

Ett yttre mått, 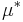\mu^*\,, är formellt en funktion definierad på potensmängden 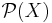\mathcal{P}(X) över en mängd 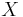X\, med värdemängd i [0,\infty] (se utökade reella tallinjen) som uppfyller följande:

  • Icke-negativitet: ingen mängd har negativt yttre mått:
\mu^* (A) \geq 0
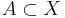för alla A \subset X;
\mu^* (\varnothing) = 0;
  • Monotonicitet: om 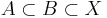A \subset B \subset X så är
\mu^*(A) \leq \mu^*(B)
  • Subadditivitet: om 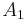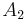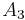A_1\,, A_2\,, A_3\,, ... är en uppräknelig följd av mängder i 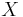X\,, så gäller
\mu^* \left(\bigcup_{i=1}^\infty A_i\right) \leq \sum_{i=1}^\infty \mu^* (A_i).

Koppling till vanliga mått

Motivationen för namnet yttre mått är att man kan definiera storleken för alla mängder. Men med några yttre mått, likaså Lebesguemåttet och Hausdorffmåttet, finns icke mätbara mängder som inte är "resonliga" att mäta. Man vill nu kunna definiera ett vanligt mått utifrån ett yttre mått.

Därför måste man sortera "dåliga" och "bra" mängder för yttre mått så at vi fåt ett mått. Vi kallar de "bra" mängderna mätbara.

Mer precist, om 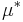\mu^*\, är ett yttre mått i 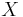X\,, kallas mängden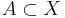 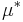A \subset X \mu^*\,-mätbar, om det för alla 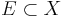E \subset X gäller att

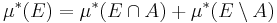{\mu}^*(E) = {\mu}^*(E \cap A) + {\mu}^*(E \setminus A)\,.

Detta kallas för Carathéodorys kriterium.

För mätbara mängder är yttre måttet samma sak som måttet. Med exakt ord, om 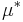\mu^*\, är ett yttre mått i 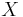X\, och

\mathcal{M}_{{\mu}^*}(X) := \lbrace A \subset X \mid A \mbox{ är } {\mu}^*\mbox{-mätbara} \rbrace ,

så är funktionen

\mu := \mu^* |\mathcal{M}_{\mu^*}(X)

ett mått, dvs 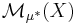\mathcal{M}_{{\mu}^*}(X) är en sigma-algebra, tomma mängden har måttet noll och 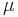\mu\, är sigma-additiv.

Eftersom alla nollmängder är 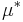\mu^*\,-mätbara så är 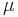\mu\, också ett fullständigt mått.

Exempel

Man använder ofta olika yttre mått, exempelvis:

Speciella yttre mått

Beroende på vilken sorts rum ett yttre mått verkar på finns det vissa egenskaper som gör det lättare att hantera, exempelvis:

  • Ett yttre mått är regelbundet, om vi kan approximera alla mängder med mätbara mängder.
  • Ett yttre mått i ett topologiskt rum är Borel om alla Borelmängder är mätbara.
  • Ett yttre mått i ett topologiskt rum är Borel-regelbundna om vi kan approximera alla mängder med Borelmängder.
  • Ett yttre mått i ett metriskt rum är metriskt om det yttre måttet är additiv för mängder som har positivt avstånd.

Konstruktion av vissa yttre mått

Huvudartikel: Carathéodorys konstruktion.

Om 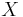X\, är ett metriskt rum kan man konstruera ett naturligt yttre mått bara med den metriska strukturen, ett förfarande som kallas Carathéodorys konstruktion. Carathéodorys konstruktion är viktig eftersom man kan konstruera ett yttre mått i alla metriska rum och dessutom konstruera många viktiga yttre mått med metoden, exempelvis yttre Hausdorffmåttet och yttre Lebesguemåttet.

Informellt skapas det yttre måttet genom att måttet (testmåttet) för en samling enkla mängder (testmängder) definieras. Ett exempel är att öppna intervall (a,b) får måttet b − a. Alla mängder E skall kunna täckas över med testmängderna. Måttet för en övertäckning är summan av måtten för testmängderna. Det yttre måttet av E är då måttet av den minsta möjliga övertäckningen (infimum).

Proceduren för att definiera ett mått blir alltså:

  1. Testmängder och ett testmått
  2. Yttre mått
  3. Mått

Se även


Postscript-viewer-blue.svg
 Detta är en sparad artikelbok.


Måtteori

Mått (matematik)
Konstruktion av en icke mätbar mängd
Definition
Yttre mått
Egenskaper hos mått
Begrepp
Nollmängd
Nästan överallt
Fullständigt mått
Integration
Mätbar funktion
Lebesgueintegration
Egenskaper hos måttintegral

Referenser

  • Halmos, P. (1950), Measure Theory, D. van Nostrand and Co.
  • Mattila, P. (1995), Geometry of Sets and Measures in Euclidean Spaces, Cambridge University Press.
Hämtad från "https://sv.rilpedia.org/wiki/Yttre_m%C3%A5tt"
Personliga verktyg