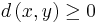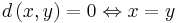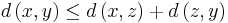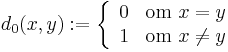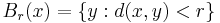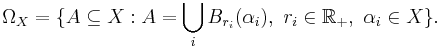Metriskt rum

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Inom matematiken är ett metriskt rum en mängd X tillsammans med en avståndsfunktion 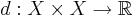d: X \times X \rightarrow \mathbb{R}

sådan att följande villkor gäller

  1. d\left(x,y\right) \ge 0
  2. d\left(x,y\right) = d\left(y,x\right)
  3. d\left(x,y\right) = 0 \Leftrightarrow x = y
  4. d\left(x,y\right) \le d\left(x,z\right) + d\left(z,y\right)

för alla element x, y och z från X.

Avståndsfunktionen betecknas vanligen d eller ρ, och kallas metrik. Om ekvivalensen i tredje villkoret ersätts med en vänsterimplikation får man en pseudometrik.

För punkter i 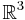\mathbb{R}^3 med den vanliga metriken är villkoren (1)-(4) uppenbara. Villkor (1) motsvarar att avståndet mellan punkter i det euklidiska rummet är positivt. Villkor (3) motsvarar att två punkter P och Q har avstånd 0 om och endast om P=Q. Villkor (4) är den så kallade triangelolikheten: för tre punkter P, Q och R gäller att avståndet mellan P och R är mindre eller lika med summan av avståndet mellan P och Q samt avståndet mellan Q och R.

Exempel

  • Varje mängd kan göras till ett metriskt rum genom att tilldela den den diskreta metriken d0:
d_0(x, y) := \left\{ \begin{array}{cc} 0 & \mathrm{om}\ x = y \\ 1 & \mathrm{om}\ x \neq y \end{array} \right.
  • \mathcal{C}[0, 1], klassen av alla kontinuerliga funktioner definierade på [0,1], blir med metriken d(f, g) = \sup\{|f(x) - g(x)|, x \in [0, 1]\} (metriken inducerad från supremumnormen) ett metriskt rum. Med samma metrik är \mathcal{C}[a,b] ett metriskt rum för alla kompakta intervall.
  • Mängden av reella tal (betecknad 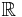\mathbb{R}) är ett metriskt rum med avståndsfunktionen d(x,y) = | x − y | .
  • Mängden 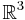\mathbb{R}^3 består av alla 3-tupler (x,y,z) där x, y och z samtliga är reella tal. Denna mängd ses konkret som punkter i det tredimensionella rummet, där 3-tupeln (a,b,c) motsvarar punkten med x-koordinat a, y-koordinat b samt z-koordinat c.
  • Mängden 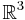\mathbb{R}^3 är ett metriskt rum med avståndsfunktionen
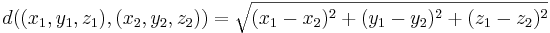d( (x_1,y_1,z_1), (x_2,y_2,z_2) ) = \sqrt{ (x_1-x_2)^2 + (y_1-y_2)^2 + (z_1-z_2)^2 } .

Denna avståndsfunktion är det avstånd som fås i rymdgeometrin genom användande av Pythagoras sats.

Topologi

Den metriska topologin i ett metriskt rum X kan definieras i form av en bas, genom att basen definieras som alla öppna bollar:

B_r(x) = \{y: d(x,y)<r\} \,

där r > 0.

Den inducerade topologin i X är alltså de mängderna som är unioner av öppna bollar:

\Omega_X = \{A\subseteq X: A = \bigcup_i B_{r_i}(\alpha_i),\ r_i\in\mathbb R_+,\ \alpha_i\in X\}.

Detta kan även formuleras som att en mängd U är öppen i den metriska topologin om det kring varje x i U existerar en öppen boll som är en delmängd till U.

Metriska rum med den metriska topologin är parakompakta Hausdorffrum. Den metriska topologin är den grövsta topologin på ett metriskt rum så att metriken 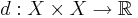d: X \times X \to \R är kontinuerlig.

Hämtad från "https://sv.rilpedia.org/wiki/Metriskt_rum"
Personliga verktyg