Kompakt
Från Rilpedia
- För skivbolaget, se Kompakt (skivbolag).
I matematiken är kompakthet en egenskap hos topologiska rum och delmängder till topologiska rum.
Innehåll |
Definition
Ett topologiskt rum X sägs vara kompakt om det varje öppen övertäckning av X har en ändlig delövertäckning. Detta innebär att om
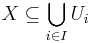 ,
,
där 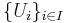 är en familj av öppna mängder, så finns
är en familj av öppna mängder, så finns 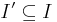 som är ändlig sådan att
som är ändlig sådan att
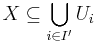 .
.
En delmängd 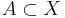 är kompakt om varje övertäckning av A med mängder som är öppna i X har en ändlig delövertäckning.
är kompakt om varje övertäckning av A med mängder som är öppna i X har en ändlig delövertäckning.
Notera att definitionerna av kompakthet varierar. Exempelvis kräver Bourbaki även att ett kompakt rum ska vara ett Hausdorffrum, och kallar topologiska rum som inte är Hausdorffrum, men som uppfyller kravet ovan, för kvasi-kompakt.
Kompakthet i olika rum
Om X är ett kompakt topologiskt rum och A är en sluten delmängd till X så är A kompakt.
En mängd i Rn är kompakt om och endast om den är sluten och begränsad. För en delmängd av ett fullständigt metriskt rum gäller att den är kompakt om och endast om den är sluten och totalt begränsad. Dessa båda resultat kallas Heine-Borels sats.
Se även
- Sigma-kompakt
- Lindelöf-rum
- Uppräkneligt kompakt
- Svagt uppräkneligt kompakt
- Pseudokompakt
- Följdkompakt
- Metakompakt
- Uppräkneligt metakompakt
- Parakompakt
- Uppräkneligt parakompakt
- Separabel
- Uppräknelig av första ordningen
- Uppräknelig av andra ordningen
Referenser
- Kelley, J.L.: General Topology, Van Nostrand, 1955.
- Steen, Lynn Arthur; J. Arthur Seebach Jr.: Counterexamples in topology, Dover Pulications, 1995.
- Hocking, John G.; Gail S. Young: Topology, Dover Pulications, 1961. ISBN 0-486-65676-4.



