Hausdorffrum

Från Rilpedia

Texten från svenska Wikipedia

Ett Hausdorffrum (även kallat T₂-rum och separerat rum) är ett topologiskt rum, i vilket två skilda punkter kan separeras med öppna mängder.

Definition

Punkterna x och y, separerade av de öppna omgivningarna U och V

Låt (X,τ) vara ett topologiskt rum, och 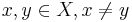. (X,τ) är ett Hausdorffrum om det existerar öppna mängder 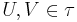sådana att 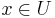, 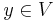och .

Exempel och motexempel

De flesta topologiska rum som studeras inom analysen är Hausdorffrum, till exempel .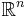

Alla metriska rum är Hausdorffrum. Pseudometriska rum är dock i allmänhet inte Hausdorffrum.

En topologi som inte är Hausdorff är Zariskitopologin som är vanligt förekommande inom den algebraiska geometrin

Egenskaper

Underrum och produkter av Hausdorffrum är Hausdorffrum. Dock är kvotrum av Hausdorffrum i allmänhet inte Hausdorffrum.

Några egenskaper som gäller för Hausdorffrum, men inte i allmänhet för topologiska rum är:

• Alla konvergenta följder och nät har ett unikt gränsvärde.
• Varje kompakt mängd är sluten