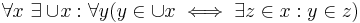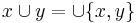Union (matematik)
Från Rilpedia
Texten från svenska Wikipedia
I matematiken är unionen mellan två mängder A och B är mängden av alla element som finns i A eller B. Med "eller" menas här inklusivt eller, dvs element som finns i både A och B ingår också i unionen. Unionen av A och B skrivs A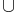 
B. Av definitionen förstår man att för alla A gäller A 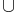ø = A och A 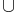A = A.
Om inklusivt eller ovan ersätts av exklusivt eller, fås den symmetrisk differensen.
Exempel:
- {A, B, C, D} 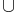{C, D, E} = {A, B, C, D, E}
- {x : x är ett jämnt tal} 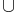{x : x är ett udda tal} = {x : x är ett heltal}
- {x : x är en människa} 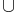{x : x är en svensk medborgare} = {x : x är en människa}
Unär union
Den ovanstående binära operatorn är dock enbart ett specialfall av den unära unionsoperatorn, som beskrivs av unionsaxiomet i mängdteorin ZFC:
Detta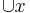 
utläses unionen av x. En vanlig beteckning är 
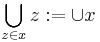, som utläses unionen av alla z i x.
Vi ser att den binära unionsoperatorn är ett specialfall, eftersom
