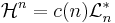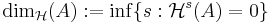Hausdorffmått
Från Rilpedia
Ett Hausdorffmått är inom matematik ett mått för metriska rum som är en generalisering av Lebesguemåttet. Hausdorffmåttet är namngett efter Felix Hausdorff som uppfann det.
Innehåll |
Bakgrund
Lebesguemåttet är definierad för en viss dimension, n, och kan bara mäta mängder som är n-dimensionella. Men där finns många mängder i matematik, likså fraktaler, som inte är n-dimensionella.
Hausdorffmåttet ses mer exakt som en geometrisk struktur för mängder. Man mäter alltid mängder med en dimension som är naturlig för en viss mängd, som kallas Hausdorffdimension.
Formell definition
Hausdorffmåttet är definierad i ett separabelt metriskt rum med ett yttre mått som kallas yttre Hausdorffmåttet.
Låt 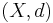 vara ett separabelt metriskt rum och s en dimension som uppfyller
vara ett separabelt metriskt rum och s en dimension som uppfyller 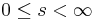 .
.
För varje 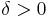 och
och 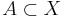 definierar vi talet
definierar vi talet
med As 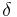 -övertäckning,
-övertäckning, 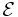 , menas att
, menas att
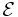 täcker A, dvs
täcker A, dvs 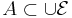
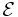 är en uppräknelig familj och
är en uppräknelig familj och- alla mängder
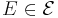 har diameter
har diameter 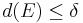 .
.
Eftersom X är separabelt finns det en 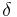 -övertäckning av X för alla
-övertäckning av X för alla 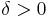 , så att
, så att
är en funktion som kallas 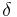 -Hausdorffinnehållet
-Hausdorffinnehållet
Dessutom, om 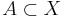 och
och  finns det mindre
finns det mindre 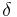 -övertäckningar för
-övertäckningar för 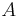 , dvs funktionen
, dvs funktionen 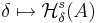 är växande när
är växande när  .
.
Därför finns gränsvärdet 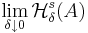 , och vi kan definiera gränsfunktionen
, och vi kan definiera gränsfunktionen
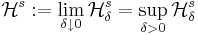 ,
,
som kallas det s-dimensionella yttre Hausdorffmåttet.
Hausdorffmåttet är det mått genererad av yttre Hausdorffmåttet över mätbara mängder definierad med Carathéodorys kriterium.
Alternativt, man kan också definiera Hausdorffmåttet med Carathéodorys konstruktion.
Egenskaper
Yttre Hausdorffmåttet är
- Ett yttre mått.
- Ett metriskt yttre mått.
- Ett Borel yttre mått.
- Ett Borel-regelbundet yttre mått.
Det finns en koppling mellan Hausdorffmåttet och andra mått.
- Nolldimensionella Hausdorffmåttet är räknemåttet.
- I
 är det n-dimensionella yttre Hausdorffmåttet det n-dimensionella yttre Lebesguemåttet utan konstant:
är det n-dimensionella yttre Hausdorffmåttet det n-dimensionella yttre Lebesguemåttet utan konstant:
där 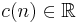 är en konstant.
är en konstant.
- I
 är det m-dimensionella yttre Hausdorffmåttet, där
är det m-dimensionella yttre Hausdorffmåttet, där  , samma sak som "areamåttet", dvs man kan mäta area för m-dimensionella mångfalder i
, samma sak som "areamåttet", dvs man kan mäta area för m-dimensionella mångfalder i 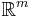 . Den här egenskaper generaliserar Lebesguemåttet: m-dimensionella mångfalder är nollmängder för Lebesguemåttet. Detta innebär att man kan få mer information om en geometrisk struktur för mängder med Hausdorffmåttet.
. Den här egenskaper generaliserar Lebesguemåttet: m-dimensionella mångfalder är nollmängder för Lebesguemåttet. Detta innebär att man kan få mer information om en geometrisk struktur för mängder med Hausdorffmåttet.
Dimension
- Huvudartikel: Hausdorffdimension.
Att det bara finns en naturlig dimension s för alla mängder i  innebär att mängdens Hausdorffmått är noll om dimensionen är mer än den naturliga dimensionen och oändlig om dimensionen är mindre än den naturlig dimensionen. Den här naturliga dimensionen kallas Hausdorffdimension, definierad som:
innebär att mängdens Hausdorffmått är noll om dimensionen är mer än den naturliga dimensionen och oändlig om dimensionen är mindre än den naturlig dimensionen. Den här naturliga dimensionen kallas Hausdorffdimension, definierad som:
för 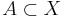 .
.
Man behöver ofta Hausdorffdimensionen inom fraktalgeometri.
Se även
Referenser
- Kenneth Falconer, Fractal geometry, John Wiley, Second Edition, 2003




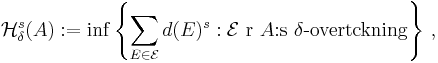
![\mathcal{H}^s_\delta : \mathcal{P}(X) \rightarrow [0,\infty],](/w/images/sv.rilpedia.org/math/9/e/c/9ec35f0f97d6595ef798d0393afd6505.png)