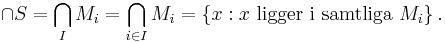Familj (matematik)
Från Rilpedia
En familj kan inom matematiken användas antingen i en speciell betydelse som en uppsättning av element med index, eller allmännare som synonym till mängd. I det senare fallet avses ofta en mängd vars element själva är mängder. I den här artikeln behandlas främst den specifika betydelsen.
Familjer generaliserar par, trippler och andra "tupler", samt följder.
Innehåll |
Enkla exempel
- Familjen (2n)n∈Z består av alla heltalspotenser av talet 2, alltså av 1, 2, 4, 8, o. s. v., men också av 1/2, 1/4 o. s. v.
- Trippeln (5, -8, 5) kan ses som en familj över indexmängden {1, 2, 3}, där indexet markeras implicit med positionen. Formellt kan alltså trippeln skrivas som (ai)i∈{1,2,3} med a1 = a3 = 5 och a2 = -8.
- Den aritmetiska talföljden 3, 7, 11, 15, 19, 23,... kan uppfattas som en familj antingen med indexmängd N eller med bara Z+ (de positiva heltalen) som indexmängd, alltså antingen som (4n+3)n∈N eller som (4n-1)n∈Z+.
Formell definition
Formellt kan en familj (ai)i∈I definieras som en funktion med indexmänden I som definitionsmängd. För varje i som tillhör I ses då ai som funktionsvärdet av i. Till skillnad från vad som brukar gälla för funktioner är man dock inte intresserad av denna funktions målmängd. Två familjer (ai)i∈I och (bi)i∈I över samma indexmängd I är lika om och endast om ai = bi för varje i i I. Om det inte finns någon risk för flertydighet, så skriver man ofta (ai)I i stället för (ai)i∈I .
Man använder ofta mängdbeteckningar i samband med familjer. Exempelvis säges ai vara ett element i eller tillhöra familjen ovan. Till skillnad från vanliga mängder kan dock samma element tillhöra en familj "flera gånger", eftersom ibland ai = aj trots att i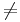 j. Ett specialfall är när alla ai är lika, alltså funktionen är en konstantfunktion, säg med det konstanta värdet c. I detta fall kan familjen kort betecknas (c)I.
j. Ett specialfall är när alla ai är lika, alltså funktionen är en konstantfunktion, säg med det konstanta värdet c. I detta fall kan familjen kort betecknas (c)I.
Ett annat specialfal är när indexmängden I = {1, 2, 3,..., n} för något positivt heltal n. I detta fall använder man oftast "tipelnotation", och skriver familjen (ai)i∈I som (a1, a2,..., an) Man kan också beteckna den 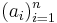 , och mer allmänt kan (ai)i∈{m,m+1,m+2,...,n} också skrivas som
, och mer allmänt kan (ai)i∈{m,m+1,m+2,...,n} också skrivas som 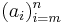 . Dessa beteckningar är dock ovanligare.
. Dessa beteckningar är dock ovanligare.
Delfamilj
En familj (bi)i∈J är en delfamilj till familjen (ai)i∈I, om J är en delmängd av I och dessutom bi = ai för varje i i J. Exempelvis kan delföljder uppfattas som delfamiljer; delföljden
- a1, a3, a5, a7, a9, a11, a13,...
av följden
- a0, a1, a2, a3, a4, a5, a6,...
ges väsentligen av att man inskränker indexmängden från N till mängden av udda naturliga tal.
Operationer på familjer
Många operatorer på element till vissa typer av familjer ger upphov till operationer på familjer. Detta kan bland annat göras genom komponentvisa operationer eller itererade operationer. Det finns också operationer som på ett väsentligare sätt samspelar med indexmängden, som cartesiska produkter och vissa typer av limes.
Komponentvisa operationer
Låt A = (ai)I och B = (bi)I vara två familjer över samma indexmängd I. Om en viss binär operator o är definierad för ai och bi för varje index i i I, så kan man definiera en familj A o B över I genom
- A o B = (aiobi)I .
Man låter alltså operatorn o verka på varje komponent för sig. Om till exempel alla ai och bi är reella tal, så kan man låta operatorn vara något av räknesätten addition, multiplikation och subtraktion. Detta ger familjerna (ai+bi)I , (aibi)I respektive (ai-bi)I .
Det finns flera varianter av komponentvisa operationer. Om exempelvis för familjerna A och B som ovan i stället för varje i ∈ I både ai och bi ligger i en grupp Gi med gruppoperationen oi, så kan man sätta
- A o B = (ai oi bi)I .
Även andra typer av operatorer kan utnyttjas, som skalär trippelprodukt eller multiplikation av skalär och vektor.
Itererade operationer
I en del fall kan man utföra en operation som kombinerar samtliga element till ett enda element av samma typ som de ursprungliga. Om exempelvis S = (Mi)_I är en familj av mängder, så kan man bilda unionen av samtliga Mi:
På liknande sätt kan man bilda skärningsmängden:
Skulle dessutom här till exempel I = {m,m+1,...,n}, så kan också beteckningarna 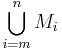 respektive
respektive 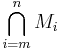 användas.
användas.
Ett annat exempel är den generaliserade summan av alla element i en familj (ai)I av ickenegativa reella tal, 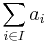 , som kan definieras som supremum av alla delsummor över ändliga delmängder av I, om detta supremum existerar, och annars som
, som kan definieras som supremum av alla delsummor över ändliga delmängder av I, om detta supremum existerar, och annars som 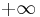 .
.
Cartesiska produkter
Om (Mi)I är en familj av mängder, så definieras deras cartesiska produkten som mängden av alla familjer (xi)I, sådana att xi ∈ Mi för varje i i I.
Direkta och inversa limes
Andra betydelser
Familj eller det motsvarande engelska ordet family används ibland även i andra betydelser. Walter Rudin anger exempelvis att han använder ordet som en av flera synonymer till (det engelska ordet för) mängd[1]. (Skillnaden mellan betydelserna är egentligen inte särskilt stor, eftersom varje mängd M formellt sett medelst identitetsavbildningen på mängden svarar mot en familj i den specifikare betydelsen, med sig själv som indexmängd. Mot M svarar alltså familjen (x)x∈M.)
Ofta betraktar man då en familj av delmängder till en mängd A, vilket är en mängd vars element är delmängder av A. Generellt är en familj av mängder en klass vars element är mängder.
Exempel på "familjer" av delmängder
- M = {{1,2},{2,3},{3,4}} är en familj av delmängder av A = {1,2,3,4}.
- Potensmängden P(A) av en mängd A är en familj av delmängder av A. Varje familj av delmängder av en mängd är själv en delmängd till potensmängden för denna mängd.
- En topologi på en mängd X bestäms av familjen av öppna delmängder till X.
- En hypergraf är en mängd V av hörn, tillsammans med en familj av delmängder till V, kanterna.
Noter
- ↑ Walter Rudin, Real and complex analysis (3:e upplagan), avsnitt 1.1.