Grupp (matematik)
Från Rilpedia
En grupp är en typ av algebraisk struktur, vars studium kallas gruppteori.
Innehåll |
Historia
Gruppteorin har tre huvudsakliga inspirationsområden; talteorin, sökandet efter lösningar av polynomekvationer och studiet av symmetrier inom geometrin. Den modulära aritmetiken gav tidiga exempel på grupper som skiljde sig från de klassiska talsystemen. Lagrange, Ruffini och Abel erhöll flera tidiga resultat om permutationsgrupper i sitt studie av lösningar till polynomekvationer av hög ordning. Termen grupp myntades av Galois i arbetet med Galoisteorin som kan besvara frågan när en polynomekvation har en lösningsformel. Felix Klein var med sitt Erlangen-program, som syftade till att reducera geometrin till studiet av symmetrier, en annan viktig föregångare.
Runt 1880 förenades dessa separata områden i gruppteorin. Denna har sedan varit inspirationskälla för skapandet av såväl abstrakt algebra som områden som reresentationsteori.
Definition
En grupp (G, •) är en mängd G tillsammans med med en binär operator • på G (det vill säga en funktion från G × G till G) som uppfyller följande villkor:
-
Associativitet. För alla a, b och c i G gäller (a • b) • c = a • (b • c). Existens av identitet. Det finns ett element e i G, kallat identiteten i G, med egenskapen e • a = a = a • e för alla a i G. Existens av inverser. För varje a i G finns ett element b i G, kallat inversen till a, med egenskapen a • b = e = b • a, där e är identiteten i G.
En konsekvens av definitionen är att identiteten i gruppen är unik, samt att inversen till varje givet element är unik. Gruppen (G, •) sägs vara kommutativ, eller vanligare abelsk, om den dessutom uppfyller följande villkor:
-
Kommutativitet. För alla a och b i G gäller a • b = b • a.
I generell gruppteori noterar man ofta gruppoperationen som multiplikation, det vill säga r • s noteras rs, inversen till s noteras s − 1. Man kan då också definiera potenser, sn som produkten av n likadana faktorer s. För negativa exponenter gäller s − n = (s − 1)n. För abelska grupper använder man ofta additiv notation, varvid gruppoperationen skrivs r + s och inversen − s. En summa  av n lika element skrivs då ns.
av n lika element skrivs då ns.
Delgrupp
En delgrupp H till en grupp (G,•) är en delmängd till G som i sig är en grupp med samma operator.
Om G är en ändlig grupp så gäller att antal element i H delar antal element i G (se Lagranges sats).
Grupphomomorfi
En grupphomomorfi från en grupp G till en grupp H är en funktion från G till H som "respekterar gruppstrukturen", det vill säga överför en produkt i en produkt. För att funktionen f från G till H skall vara en homomorfi krävs alltså precis att
- f(ab) = f(a)f(b)
för alla a och b i G.
Isomorfi
Två grupper (G, * ) och 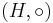 kallas isomorfa om det finns en gruppisomorfi mellan dem, det vill säga en bijektiv avbildning
kallas isomorfa om det finns en gruppisomorfi mellan dem, det vill säga en bijektiv avbildning 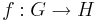 sådan att
sådan att 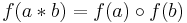 . Noteras ofta
. Noteras ofta 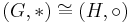 . Isomorfi är en ekvivalensrelation och delar alltså upp klassen av alla grupper i ekvivalensklasser. Ur en abstrakt synvinkel ser man isomorfa grupper som en och samma grupp.
. Isomorfi är en ekvivalensrelation och delar alltså upp klassen av alla grupper i ekvivalensklasser. Ur en abstrakt synvinkel ser man isomorfa grupper som en och samma grupp.
Viktiga klasser av grupper
En ändlig grupp är en grupp med ändligt många element. Antalet element kallas gruppens ordning.
Den cykliska gruppen genererad av ett element a består av alla potenser av a. Noteras ofta 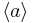 . Varje cyklisk grupp är isomorf med antingen
. Varje cyklisk grupp är isomorf med antingen 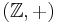 eller
eller 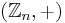 genom att
genom att 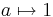 definierar en isomorfism.
definierar en isomorfism.
Den symmetriska gruppen Sn är gruppen av alla permutationer av en mängd med n element. Varje grupp är isomorf med en delgrupp till den symmetriska grupp som består av permutationer av gruppen själv.
Exempel
- Heltalen
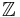 med addition, betecknas
med addition, betecknas 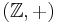 , är en oändlig cyklisk grupp som genereras av 1 eller -1.
, är en oändlig cyklisk grupp som genereras av 1 eller -1. - De nollskilda rationella talen
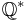 med multiplikation, betecknas
med multiplikation, betecknas 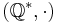
- De nollskilda reella talen
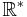 med multiplikation, betecknas
med multiplikation, betecknas 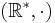
- De nollskilda komplexa talen
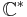 med multiplikation, betecknas
med multiplikation, betecknas 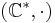
- Talen
 och addition modulo n, betecknas
och addition modulo n, betecknas 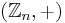 , är en ändlig cyklisk grupp. Varje element som är relativt primt med 'n' genererar gruppen.
, är en ändlig cyklisk grupp. Varje element som är relativt primt med 'n' genererar gruppen.
Operationer på grupper
Kvotgrupper
Givet en grupphomomorfi 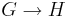 kan man visa att bilden av homomorfin utgör en delgrupp till H, samt att kärnan K, det vill säga de element i G som avbildas på enhetselementet i H, utgör en delgrupp till G.
kan man visa att bilden av homomorfin utgör en delgrupp till H, samt att kärnan K, det vill säga de element i G som avbildas på enhetselementet i H, utgör en delgrupp till G.
Det visar sig att bilden kan återskapas upp till isomorfi enbart utifrån G och delgruppen K, nämligen som kvotgruppen av G med avseende på K. Mer allmänt kan man alltid givet en grupp G och en s.k normal delgrupp N konstruera kvoten G/N enligt följande:
Låt N vara en delgrupp till G. Givet ett element 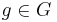 definierar vi den vänstra sidoklassen gN till N med avseende på g som mängden av element på formen gn för något element
definierar vi den vänstra sidoklassen gN till N med avseende på g som mängden av element på formen gn för något element 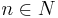 , samt den högra sidoklassen Ng som mängden av element på formen ng gör något element
, samt den högra sidoklassen Ng som mängden av element på formen ng gör något element 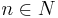 . Man kan visa att varje element i g kommer att tillhöra en och endast en vänster- respektive höger sidoklass.
. Man kan visa att varje element i g kommer att tillhöra en och endast en vänster- respektive höger sidoklass.
Delgruppen N sägs vara normal om för varje g så gäller gN=Ng.
För en normal delgrupp N till G definieras nu kvotgruppen G/N som mängden av sidoklasser tillsammans med den operation som ges av gN*g'N=gg'N. Man kan visa att detta ger en väldefinierad operation.
Det finns nu en naturlig grupphomomorfi 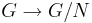 som ges av
som ges av 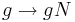 . N kommer att vara kärnan för denn homomorfi, och G/N är bilden.
. N kommer att vara kärnan för denn homomorfi, och G/N är bilden.
Direkt produkt av grupper
Givet två grupper G och H kan man definiera deras direkta produkt 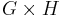 som mängden av par
som mängden av par 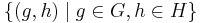 med operationen (g,h)*(g',h')=(gg',hh'). Enhetselementet utgörs av (eG,eH) och inversen till (g,h) ges av (g − 1,h − 1). Från
med operationen (g,h)*(g',h')=(gg',hh'). Enhetselementet utgörs av (eG,eH) och inversen till (g,h) ges av (g − 1,h − 1). Från 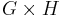 finns nu projektionsavbildningar till G respektive H vars kärna är H respektive G, så att H är kvoten av
finns nu projektionsavbildningar till G respektive H vars kärna är H respektive G, så att H är kvoten av 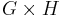 med undergruppen
med undergruppen 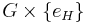 och vice versa.
och vice versa.