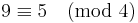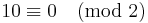Kongruens modulo

Från Rilpedia

(Omdirigerad från Modulo)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Kongruens modulo är en ekvivalensrelation inom matematiken.

Två tal a och b sägs vara kongruenta modulo n om de har samma rest vid division med n.

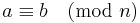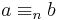Detta betecknas $a \equiv b \pmod n$ . Man kan också skriva $a \equiv_n b$ .

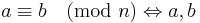$a \equiv b \pmod n \Leftrightarrow a, b$ har samma rest vid division med n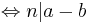 $\Leftrightarrow n | a-b$

Exempel

$9 \equiv 5 \pmod 4$

eftersom 9 och 5 båda ger resten 1 vid division med 4.

$10 \equiv 0 \pmod 2$

eftersom 10 och 0 ger samma rest (0) vid division med 2.

Generaliseringar

Om man låter $(n)$ beteckna delmängden 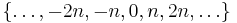$\{\ldots, -2n, -n, 0, n, 2n, \ldots\}$ av Z, så kan ovanstående definition formuleras 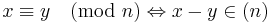$x \equiv y \pmod{n} \Leftrightarrow x - y \in (n)$ . Den avgörande egenskapen hos $(n)$ är att den är ett ideal. Man låter ofta 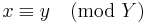$x \equiv y \pmod{Y}$ betyda 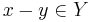$x-y\in Y$ där $Y$ är ett ideal i en ring $X$ , eller allmänare Y är en delmodul av en modul X. Mängden av ekvivalensklasser till denna relation betecknas $X / Y$ , och kallas en kvotring (respektive kvotmodul, kvotgrupp, kvotrum och så vidare).