Moduloräkning
Från Rilpedia
 |
En eller flera användare anser att denna text bör infogas i Kongruens modulo. (Diskussion) |
Moduloräkning (även kallat kongruensräkning) är ett område inom elementär algebra. Relationen kongruens modulo används bland annat för datoraritmetik och inom kryptering.
Innehåll |
Inledning
Två tal a och b är kongruenta modulo n om de ger samma rest vid division med n (a,b och n är heltal, n är större eller lika med 2).
Detta betecknas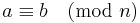 
. Man kan också skriva 
.
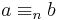Om a och b inte är kongruenta modulo n, säger vi att talen är inkongruenta.
Vilket betecknas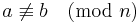 
Exempel
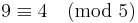, Resten kan i båda fallen bli 4 vid division med 5
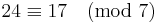, Resten kan i båda fallen bli 3 vid division med 7
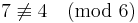, Resten blir olika vid division med 6
De fyra räknesätten
Vid moduloräkning fungerar addition, subtraktion och multiplikation som vanligt. Division fungerar bara i vissa fall, därför bör man undvika det, istället kan man förkorta enligt angiven moduloklass och sedan multiplicera för att ta sig runt problemet.
Addition
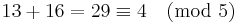
Om vi ersätter talen ovan med andra tal som är kongruenta med de första så får vi samma svar
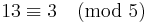
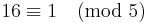
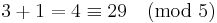
Subtraktion
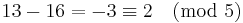
Om vi ersätter talen ovan med andra tal som är kongruenta med de första så får vi samma svar
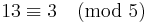
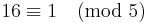
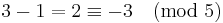
Multiplikation
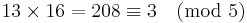
Om vi ersätter talen ovan med andra tal som är kongruenta med de första så får vi samma svar
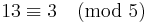
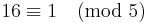
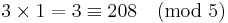
Division
Som tidigare nämnts, så fungerar division bara i vissa fall, därför bör man undvika det. Istället kan man förkorta enligt angiven moduloklass och sedan multiplicera för att ta sig runt problemet.
Referenser
Tryckta källor
A. Asratian, A. Björn, B. O. Turesson: Diskret Matematik, Matematiska institutionen, Linköpings Universitet, Linköping 2007.
Webbkällor
http://www.peterholgersson.se/pdf.php?d=405 (hämtad 2008-05-12)
