Från Rilpedia

En normal delgrupp är inom abstrakt algebra en speciell sorts delgrupp som är viktiga vid konstruktionen av kvotgrupper. Évariste Galois var den förste att inse vikten av existensen av normala delgrupper.

Definition

Om G är en grupp och N en delgrupp till G så är N en normal delgrupp till G om elementen i N är invarianta under konjugation, dvs N är normal om, för alla h i N och alla g i G så är ghg ^{− 1} ett element i N. Att N är en normal delgrupp till G skrivs oftast 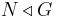eller .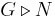

Följande utsagor är ekvivalenta och vilken som av dem kan användas som definition för normal delgrupp:

• 
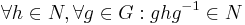
• N:s vänstersidoklasser och högersidoklasser är samma.
• Det existerar någon homomorfi på G som har N som kärna.

En normal delgrupp M säges vara en maximal normal delgrupp i G om M ≠ G och det inte finns någon normal delgrupp N i G så att M < N < G.

Exempel

• Mängden som endast innehåller det neutrala elementet, {e}, och hela G är alltid normala delgrupper till G. Dessa delgrupper säges vara de triviala delgrupperna; om de triviala delgrupperna är de enda normala delgrupperna säges G vara en enkel grupp.
• Om G är en abelsk grupp är alla delgrupper normala, ty gN = Ng. En grupp som inte är abelsk där alla delgrupper är normala kallas hamiltonsk grupp.

Egenskaper

• Normalitet bevaras av surjektiva homomorfier.
• Normalitet är inte en transitiv relation, en normal delgrupp till en normal delgrupp till G behöver inte vara normal i G.
• Om en delgrupp N till G är normal kan man bilda kvotgruppen G / N, ty man kan definiera multiplikation av sidoklasser enligt:

(aN)(bN) = abN

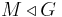• är maximal om och endast om G / M är enkel.