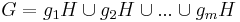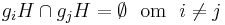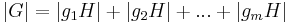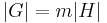Lagranges sats
Från Rilpedia
Lagranges sats är en matematisk sats inom abstrakt algebra. Satsen lyder att om G är en ändlig grupp och H är en delgrupp till G så är ordningen för H en delare till ordningen för G. Satsen är uppkallad efter Joseph-Louis Lagrange.
Bevis
Alla vänstersidoklasser till undergruppen H bildar en partition av G:
och då storleken av en union av parvis disjunkta mängder är summan av storleken på de ingående mängderna får man att:
Då en egenskap hos vänstersidoklasser är att varje sidoklass innehåller lika många element som undergruppen den konstruerades ifrån, | giH | = | H | , får man att
vilket skulle bevisas.
Följder av Lagranges sats
Lagranges sats ger att alla delgrupper till en grupp måste ha en ordning som delar gruppens ordning. Det omvända gäller dock inte, det vill säga att det måste inte finnas en delgrupp till varje delare till gruppens ordning.
För alla element 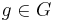 är ordningen av g, o(g), en delare i | G | .
är ordningen av g, o(g), en delare i | G | .
För alla ändliga grupper G med ordning n gäller att gn är det neutrala elementet för alla element g i G.
Alla grupper med primtalsordning, det vill säga gruppens ordning är ett primtal, är cykliska grupper.