Från Rilpedia

I matematiken är en Liegrupp en differentierbar mångfald med en differentierbar gruppstruktur, dvs en differentierbar mångfald M tillsammans med differentierbara funktioner 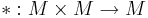och 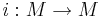samt en punkt 0 sådana att (M,*,i,0) är en grupp; där 0 är identitetselementet och i är inversavbildningen .

Exempel:

1. Den additiva gruppen av reella tal är en Liegrupp
2. Gruppen av 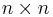-matriser över R med determinant 1 är en Liegrupp under multiplikation, eftersom den kan betraktas som en delmångfald till 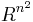och matrismultiplikation respektive matrisinversion är differentierbara avbildningar.