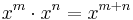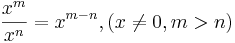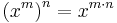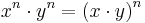Potens (matematik)

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Ett uttryck av typen 45 kallas för en potens med basen 4 och exponenten 5, och utläses "fyra upphöjt till fem". Ofta talar man om uttryck på formen ab som potensuttryck. Operationen att "upphöja" kallas exponentiering. I sammanhang där det är typografiskt omöjligt att skriva upphöjda siffror, liksom i programmeringssammanhang och på många miniräknare, förekommer även skrivsättet a^b.

Innehåll

Definitioner

Definition 1

I sin enklaste form (som tidigare kallades dignitet) definierar man potenser som resultatet av upprepad multiplikation. Exempelvis, 43 (utläses 4 upphöjt till 3) blir 4 · 4 · 4 = 64.

Omvänt så blir kubikroten ur 64 = 4 (Roten ur 64 ≠ 16 och roten ur 16 = 4).

I den här definitionen förutsätts att exponenten är ett positivt heltal.

Potenslagarna

Ur definitionen av potenser med positiva tal som heltalsexponent kan man härleda följande räkneregler, potenslagarna:

  • x^m \cdot x^n = x^{m+n}
  • {x^m \over x^n} = x^{m-n}, (x \ne 0, m>n)
  • {(x^m)}^n = x^{m \cdot n}
  • x^n \cdot y^n = {(x \cdot y)}^n

Utgående från dessa lagar definieras sedan utvidgade betydelser av potens.

Definition 2

Med utgångspunkt i att potenslagarna skall gälla även när exponenten är ett negativt heltal inför man definitionerna att

  • a0 = 1 (om a ≠ 0) Exempel: 20 = 1
  • a−n = 1 / an (om a ≠ 0). Exempel: 2−1 = 1 / 21

För a = 0 går det inte att ge en definition för ax annat än om x>0. Speciellt hör uttrycket 00 till de odefinierbara uttrycken.

Definition 3

För att den tredje potenslagen ska fungera, definieras värdet av potenser med rationella exponenter

  • x = a p/q (där a > 0) är det positiva tal x som uppfyller xq = ap

Speciellt betecknas a1/2 som (kvadrat)roten ur a (skrives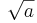\sqrt a) och a1/3 som kubikroten ur a (skrives \sqrt[3] a).

Definition 4

Om exponenten är irrationell, dvs reell men inte rationell, utgår man från kontinuitetsprincipen:

Om x1<y<x2 så ska ax1<ay<ax2 gälla (där a>1), och genom att låta x2 − x1 bli allt mindre, bestäms ay som ett gränsvärde. (Om 0<a<1 gäller omvända olikheter.)

Vanligen definierar man ax = ex ln a

Definition 5

För komplexa tal (och därmed även för negativa reella baser) kan man skriva om potensuttrycket, så att det kan återföras på följande definition (se Eulers formel):

  • eiφ = cosφ + isinφ
Wiki letter w.svg  Detta korta avsnitt behöver utökas.

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Potens_(matematik)"
Personliga verktyg