Ahlfors-regelbundet mått
Från Rilpedia
Ett Ahlfors-regelbundet mått är inom matematik ett mått i ett metriskt rum som beter sig som Lebesguemåttet. Måttet är uppkallat efter finska matematikern Lars Ahlfors.
Innehåll |
Definition
Låt 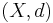 vara ett metriskt rum. Ett Radonmått
vara ett metriskt rum. Ett Radonmått 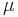 i
i 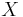 är s-Ahlfors-regelbundet om det finns
är s-Ahlfors-regelbundet om det finns 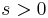 och
och 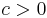 så att
så att
för alla 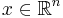 och
och 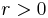 . Br(x) är bollen med mittpunkt x och radie r.
. Br(x) är bollen med mittpunkt x och radie r.
Exempel
Det n-dimensionella Lebesguemåttet är n-Ahlfors-regelbundet eftersom det är ett Radonmått och för alla 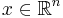 och
och 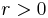
där 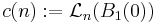 .
.
Geometrisk struktur och Ahlfors-regelbundet rummet
Om man kan definiera ett Ahlfors-regelbundet mått i ett metriskt rum, är detta måttstrukturen i det metriska rummet och storleken beter sig på samma sätt som i 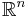 .
.
Till exempel, om det finns ett s-Ahlfors-regelbundet mått i det metriska rummet (X,d) så är
- Man kan skala måttet för mindre mängder:
 ,
,
precis som i 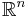 .
.
Om man kan definiera ett Ahlfors-regelbundet mått i ett metriskt rum X så är X Ahlfors-regelbundet rummet. Därför till exempel  är Ahlfors-regelbundet.
är Ahlfors-regelbundet.
Se även
Referenser
- P. Halmos, Measure theory, D. van Nostrand and Co., 1950.




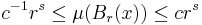
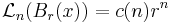
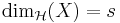 ,
,