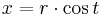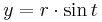Från Rilpedia

En cirkel är en perfekt rund kurva. Formellt definieras cirkeln som den mängd av punkter i planet som ligger på ett bestämt avstånd, cirkelns radie, från en bestämd punkt, cirkelns mittpunkt. Radien är alltså avståndet från mittpunkten till vilken punkt som helst på cirkeln.

I dagligt tal och i delar av skolmatematiken används begreppet cirkel också för att benämna det område som cirkeln omsluter. Detta område benämns i vedertagen matematisk terminologi som en cirkelskiva.

I tre dimensioner är sfären en naturlig analogi till cirkeln. Även i högre dimensioner används ordet sfär för en mängd av punkter på konstant avstånd till en given punkt.

Innehåll 1 Begrepp 2 Cirkelns ekvation 3 Cirkeln som en slät kurva 4 Cirkeln i Euklidisk geometri 5 Se även

Begrepp

• Längden på den kurva som en cirkel utgör kallas för cirkelns omkrets. En sträcka som går mellan två punkter på cirkeln via mittpunkten kallas för en diameter i cirkeln. Även längden på en sådan sträcka kallas diameter. En linje som går från en punkt till en annan på cirkeln kallas korda.
• En punkt som ligger i det område som en cirkel omsluter, men inte på cirkeln, sägs ligga i det inre av cirkeln. En punkt på själva cirkeln sägs ibland vara en punkt på periferin.
• En cirkel som går genom samtliga hörn på en given triangel sägs vara en omskriven cirkel. En cirkel som tangerar samtliga sidor på en triangel sägs vara en inskriven cirkel.
• En vinkel mellan två kordor AB,BC sägs vara en periferivinkel. En vinkel mellan två radier AM, MB sägs vara en mittpunktsvinkel.
• En sammanhängande del av cirkelns båge kallas för en cirkelbåge.
• En sammanhängande sektor av cirkeln kalla cirkelsektor.

Cirkelns ekvation

I ett koordinatsystem kan en cirkel med mittpunkt i (x₀,y₀) och radie r beskrivas som mängden av punkter som uppfyller följande ekvation:

(x − x₀)² + (y − y₀)² = r².

Ekvationen inses genom att nyttja Pythgoras sats för att beräkna avståndet från punkten (x₀,y₀) till punkten (x,y).

Arean på cirkeln, cirkelskivan, är A = πr². Omkretsen är O = 2πr. Omkretsen fås genom derivering av arean.

Cirkeln som en slät kurva

Cirkeln kan beskrivas som en slät, parametriserad kurva på flera sätt. Till exempel ges en cirkeln med mittpunkt i origo och radie r av parametriseringen:

För r=1 får man enhetscirkeln, det vill säga cirkeln med radie 1 och mittpunkt i origo. Med hjälp av en sådan analytisk beskrivning av cirkeln kan man visa att kvoten mellan en cirkels omkrets och dess radie är en konstant, alltså oberoende av vilken cirkel man väljer. Talet π definieras som halva denna kvot. Man kan också visa analytiskt att det område som cirkeln omsluter är πr². Detta kallas ofta något oegentligt för cirkelns area.

Cirkeln i Euklidisk geometri

Cirkeln är ett primitivt objekt i den euklidiska geometrin, och introduceras i axiomet som säger att givet en sträcka, så finns en cirkel med mittpunkt i en av sträckans ändpunkter och med sträckan som radie. Cirklar används bland annat för att konstruera räta vinklar, och för att dela sträckor i två delar. Vidare finns ett antal satser i euklidisk geometri om cirklars egenskaper:

• Om A, B och C är punkter på en cirkel och AC är en diameter, så är vinkeln ABC rät.
• För varje triangel finns en och endast en omskriven cirkel.
• För varje triangel finns en och endast en inskriven cirkel.
• Om A,B,C,D är punkter på en cirkel och M skärningspunkten mellan kordorna AB och CD, så gäller att |AM||MB|=|CM||MD|

Se även

• Cirkelresonemang
• Cirkelargumentation
• Cirkeldefinition