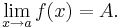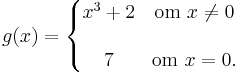Gränsvärde
Från Rilpedia
- Denna artikel handlar om det matematiska begreppet gränsvärde. Se också Gränsvärde (hygieniskt).
Ett gränsvärde för en funktion beskriver hur funktionen beter sig när dess argument kommer nära en viss punkt eller växer sig större och större. Gränsvärden används i Matematisk analys, bland annat för att definiera de viktiga koncepten kontinuitet och derivata.
Gränsvärdet betecknas med notationen:
alternativt 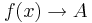 då
då 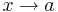 .
.
Båda utläses som ”gränsvärdet av f(x) då x går mot a är lika med A” eller ”limes av f(x) …”, och innebär att när x är "nästan" a kommer f(x) att "nästan" vara A. Viktigt att notera är att f(a) inte behöver vara definierad, och om f(a) är det, behöver det inte nödvändigtvis vara lika med A.
Exempel: Låt f(x)=x³+2. Vi är intresserade av gränsvärdet då 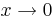 . Ett sätt att ta reda på detta som egentligen inte är helt matematiskt korrekt men som är en bra illustration är att göra en värdetabell:
. Ett sätt att ta reda på detta som egentligen inte är helt matematiskt korrekt men som är en bra illustration är att göra en värdetabell:
| f(-1) | f(-0,1) | f(-0,01) | f(0) | f(0,01) | f(0,1) | f(1) |
| 1 | 1,999 | 1,999999 | 2 | 2,000001 | 2,001 | 3 |
Eftersom funktionen tycks närma sig värdet "2" från både höger och vänster så är detta gränsvärdet. Att f(0) faktiskt är 2 har inget med saken att göra. Nedanstående funktion har faktiskt precis samma gränsvärde när x går mot 0:
Det finns dock naturligtvis funktioner för vilka det är långt mer komplicerat att beräkna gränsvärdet. I allmänhet är dessa sådana att man får uttryck på en obestämd form om man försöker sätta in funktionsvärden direkt, som till exempel "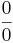 " (se division med noll), "
" (se division med noll), "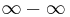 " eller "
" eller "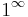 ".
".
Exempel: Funktionen f(x) = sin(x) / x är inte definierad för x = 0 eftersom division med noll inte är definierat. Däremot är gränsvärdet av f(x) då 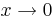 lika med 1.
lika med 1.
Det är inte alltid ett gränsvärde existerar; till exempel existerar inte gränsvärdet av 1 / | x | då 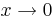 eftersom värdet går mot oändligheten. Detta skrivs ibland något oegentligt som att gränsvärdet är oändligheten. Inte heller gränsvärdet av sin(x) då
eftersom värdet går mot oändligheten. Detta skrivs ibland något oegentligt som att gränsvärdet är oändligheten. Inte heller gränsvärdet av sin(x) då 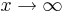 existerar eftersom funktionen oscillerar kring noll utan någon tendens att plana ut. Ett annat exempel är
existerar eftersom funktionen oscillerar kring noll utan någon tendens att plana ut. Ett annat exempel är 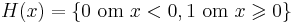 , som inte har något gränsvärde för x = 0. Gränsvärdena från vänster och höger finns dock, med värdena 0 och 1.
, som inte har något gränsvärde för x = 0. Gränsvärdena från vänster och höger finns dock, med värdena 0 och 1.
Strikt definition
Ett reellt tal (A) är ett gränsvärde för funktionen f(x) då dess argument (x) närmar sig det reella talet a, om man kan få det reella talet f(x) att ligga hur nära talet A som helst, bara man ser till att talet x ligger tillräckligt nära talet a.
Säg att vi vill att f(x) skall befinna sig inom avståndet 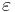 från talet A, det vill säga att absolutbeloppet
från talet A, det vill säga att absolutbeloppet 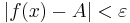 . Då måste vi se till att talet x ligger tillräckligt nära talet a; hur nära beror på avståndet
. Då måste vi se till att talet x ligger tillräckligt nära talet a; hur nära beror på avståndet 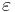 , och vi kallar detta avstånd för
, och vi kallar detta avstånd för 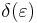 . Alltså: Om avståndet mellan talen x och a är mindre än avståndet
. Alltså: Om avståndet mellan talen x och a är mindre än avståndet 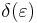 , så kommer avståndet mellan talen f(x) och A att vara mindre än avståndet
, så kommer avståndet mellan talen f(x) och A att vara mindre än avståndet 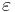 .
.
Formellt skriver man detta på följande sätt.
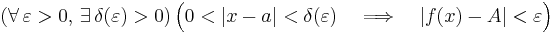 .
.
Alternativ definition
Det finns även en alternativ definition av gränsvärde där man i ovanstående ersätter 0 < | x − a | < δ med | x − a | < δ. Denna definition förekommer i boken "Analys i en variabel" av Arne Persson och Lars-Christer Böiers. Man bör dock vara medveten om att denna alternativa definition inte är allmänt accepterad.
Om funktionen inte är definierad i a finns ingen skillnad mellan de två definitionerna, men om funktionen är definierad i a skärper den alternativa definitionen kraven på A och f så att det även krävs att funktionsvärdet f(a) ska sammanfalla med gränsvärdet A, d.v.s. att f ska vara kontinuelig i a.
Se även