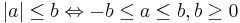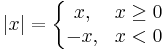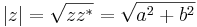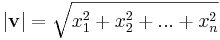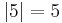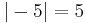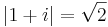Absolutbelopp
Från Rilpedia
Absolutbeloppet, eller absolutvärdet av ett tal 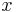 betecknas
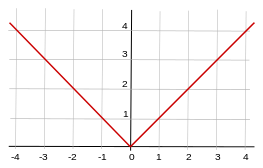
betecknas 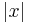 och är ett positivt reellt tal eller noll och kan ges den geometriska tolkningen som ett tals avstånd till origo eller 0-punkten i det fall talet kan representeras på tallinjen.
och är ett positivt reellt tal eller noll och kan ges den geometriska tolkningen som ett tals avstånd till origo eller 0-punkten i det fall talet kan representeras på tallinjen.
Absolutbeloppet av ett reellt tal 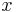 definieras av
definieras av
Absolutbeloppet av ett komplext tal 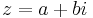 definieras av
definieras av
(se kvadratrot och komplexkonjugat.)
För en vektor 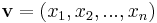 , motsvarar vektorns längd vektorns absolutbelopp:
, motsvarar vektorns längd vektorns absolutbelopp:
Längden för en vektor svarar dock vanligen mot dess norm, vilken betecknas 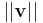 .
.
Egenskaper
Om a och b är komplexa tal gäller att:
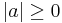
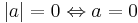
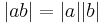
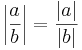
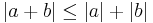 (triangelolikheten)
(triangelolikheten)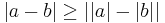 (omvända triangelolikheten)
(omvända triangelolikheten)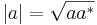 , där
, där 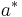 betyder komplexkonjugat.
betyder komplexkonjugat.
Om a och b är reella gäller även
- 8.