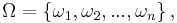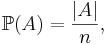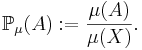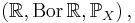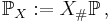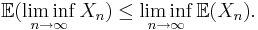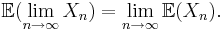Sannolikhetsrum
Från Rilpedia
Ett sannolikhetsrum är inom sannolikhetsteori ett begrepp som samlar ihop begreppen utfall, händelse och sannolikhet. Sannolikhetsrum definierades av Andrej Kolmogorov under 1930-talet.
Innehåll |
Definition
Låt 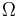 vara en icke-tom mängd och
vara en icke-tom mängd och 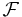 en sigma-algebra i
en sigma-algebra i 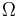 . En funktion
. En funktion ![\mathbb{P} : \mathcal{F} \longrightarrow [0,1]](/w/images/sv.rilpedia.org/math/2/4/5/2459aa295539bcf7cfac3d7f103293be.png) är ett sannolikhetsmått eller sannolikhet på sigma-algebran
är ett sannolikhetsmått eller sannolikhet på sigma-algebran 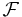 om den besitter de två egenskaperna:
om den besitter de två egenskaperna:
- Funktionen
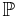 är ett mått
är ett mått 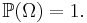
Ett sannolikhetsrum är en trippel 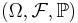 .
. 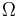 är utfallsrummet och elementen i sigma-algebran kallas händelser.
är utfallsrummet och elementen i sigma-algebran kallas händelser.
Notera att ett sannolikhetsmått är en reellvärd mängdfunktion, eftersom den avbildar en mängd, 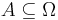 , på ett reellt tal,
, på ett reellt tal, 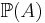 (sannolikheten för händelsen A).
(sannolikheten för händelsen A).
Tillämpningar
Sannolikhetsrum är en effektiv struktur för att beskriva många praktiska sannolikhetsproblemen.
Klassiska sannolikhetsrum
- Huvudartikel: Klassisk sannolikhetsdefinition
Man kan beskriva den klassiska sannolikhetsdefinitionen med ett sannoklikhetsrum. Då blir utfallsrummet
där 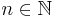 och sannolikhetsmåttet är
och sannolikhetsmåttet är ![\mathbb{P} : \mathcal{P}(\Omega) \longrightarrow [0,1]](/w/images/sv.rilpedia.org/math/e/7/c/e7c6eacea2021435025d10c7f6c375b9.png) ,
,
där | A | är kardinaliteten för mängden A.
Geometriska sannolikhetrum
- Huvudartikel: Geometrisk sannolikhetsdefinition
Om 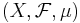 är ett måttrum där
är ett måttrum där 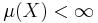 kan man definiera ett sannolikhetsmått
kan man definiera ett sannolikhetsmått ![\mathbb{P}_\mu : \mathcal{F} \longrightarrow [0,1]](/w/images/sv.rilpedia.org/math/4/3/a/43abd19d5e8f2b8a0aca64ee3a3c89aa.png) ,
,
Det geometriska sannolikhetsrummet för måttet 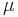 är en trippel
är en trippel 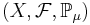 .
.
Ofta använder man 1-, 2- eller 3-dimensionella Lebesguemåttet i mängden.
Om 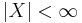 ,
, 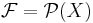 och
och 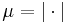 (kardinalitet som är ett mått), så är den geometriska sannolikheten samma som klassiska sannolikheten.
(kardinalitet som är ett mått), så är den geometriska sannolikheten samma som klassiska sannolikheten.
Sannolikhetsfördelningrum
- Huvudartikel: Sannolikhetsfördelning
Man kan beskriva sannolikhetsfördelningar med ett sannoklikhetsrum. Låt 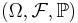 vara ett sannolikhetsrum och
vara ett sannolikhetsrum och 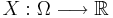 en stokastisk variabel. Sannolikhetsfördelningrummet för X är
en stokastisk variabel. Sannolikhetsfördelningrummet för X är
där
dvs utfallsrummet är reella talen, händelserna är Borelmängder och sannolikhetsmåttet är 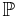 :s bildmått
:s bildmått 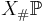 med avseende på X och kallas X:s sannolikhetsfördelning.
med avseende på X och kallas X:s sannolikhetsfördelning.
Förteckningar
Bara med måtteoretiska definitioner man kan definiera många naturlig förteckningar inom sannolikhetsteori.
Stokastisk variabel
- Huvudartikel: Stokastisk variabel
Stokastik variabel är en mätbar funktion med avseende på sannolikhetmåttet.
Mer precist, låt 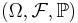 vara ett sannolikhetsrum. En funktion
vara ett sannolikhetsrum. En funktion 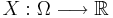 är en stokastisk variabel om
är en stokastisk variabel om
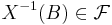 för alla Borelmängder
för alla Borelmängder 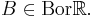
Detta innebär att en funktion 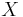 är
är 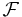 -mätbara.
-mätbara.
Väntevärde
- Huvudartikel: Väntevärde
Väntevärde för en stokastik variabel är en måttintegral med avseende på sannolikhetmåttet.
Mer precist, om låt 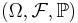 vara ett sannolikhetsrum. Om
vara ett sannolikhetsrum. Om 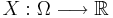 är en stokastisk variabel så är en väntevärde för X ett tal
är en stokastisk variabel så är en väntevärde för X ett tal
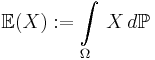 .
.
Här är 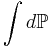 en måttintegral med avseende på måttet
en måttintegral med avseende på måttet 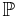 .
.
Varians och kovarians
Man kan definiera en varians och en konvarians med väntevärde.
Variansen för ett stokastisk variabel 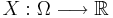 , med
, med 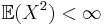 , är talet
, är talet
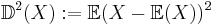 ,
,
och kovarians mellan två stokastiska variabeler 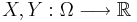 är ett tal
är ett tal
![\mbox{Cov}(X,Y) := \mathbb{E}[(X - \mathbb{E}(X))(Y - \mathbb{E}(Y))]](/w/images/sv.rilpedia.org/math/6/b/d/6bd7e8843deefb36fb7fe95a495e4428.png) .
.
Konvergenssatser
Eftersom sannolikhetsmåttet är ett mått och stokastiska variabeler är mätbara får man alla konvergenssatser också för sannolikhetsrummet.
Händelsekonvergenssatsen:
- Om
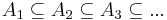 är händelser så är
är händelser så är
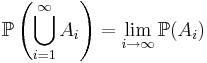 .
.
- Om
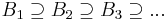 är händelser så är
är händelser så är
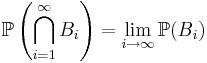 .
.
Fatous lemma: om 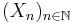 är stokastiska variabler får man att
är stokastiska variabler får man att
Monotona konvergenssatsen: om 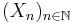 är stokastiska variabler med
är stokastiska variabler med 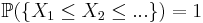 finns det
finns det 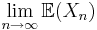 och
och
Dominerade konvergenssatsen: om 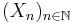 och
och 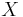 är stokastiska variabler med
är stokastiska variabler med 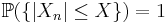 för alla
för alla 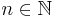 och
och 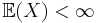 finns det
finns det 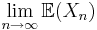 och
och