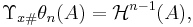Vridningsinvariant mått

Från Rilpedia

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Ett vridningsinvariant mått är inom matematiken ett mått i ortogonalgruppen.

Innehåll

1 Formell definition
2 Exempel
3 Egenskaper
4 Se även

Formell definition

Ortogonalgruppen O(n) är en lokalt kompakt topologisk grupp, så det finns ett unikt Haarmått $θ n$ i O(n):

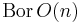$\theta_n : \mbox{Bor}\,O(n) \rightarrow [0,\infty],$

där $\mbox{Bor}\,O(n)$ är Borelalgebran i O(n). Det här mått kallas för ett vridningsinvariant mått.

Exempel

Namnet vridning har en intuitiv förklaring: Om n = 2 så är ortogonalgruppen O(2) mängden av alla vridningar och reflektioner i 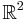$\R^2$ (se ortogonalmatris). Så att man kan identifiera det vridningsinvariant måttet 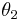$\theta_2\,$ som det utan konstant 1-dimensionella Hausdorffmåttet, dvs längdmåttet, i sfären $S^1\,$ .

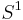Egenskaper

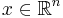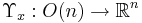Det finns ett samband mellan Hausdorffmåttet och vridningsinvarianta måttet. Låt $x \in \R^n$ och $\Upsilon_x : O(n) \rightarrow \R^n$ ,

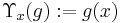$\Upsilon_x (g) := g(x)\,$ ,

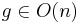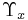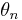för $g \in O(n)\,$ . Så att $\Upsilon_x\,$ är en $\theta_n\,$ -mätbar funktion och

$\Upsilon_{x\#} \theta_n (A) = \mathcal{H}^{n-1} (A),\,$

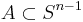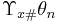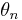för $A \subset S^{n-1}\,$ och $\Upsilon_{x\#} \theta_n\,$ är $\theta_n\,$ bildmåttet med avseende på 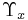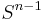$\Upsilon_x\,$ . $S^{n-1}\,$ är den n-dimensionella sfären.

Se även

Vridningsinvariant mått

Från Rilpedia

Innehåll

Formell definition

Exempel

Egenskaper

Se även

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda