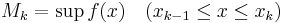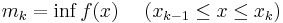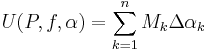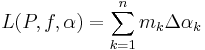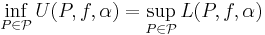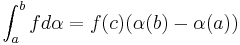Riemann-Stieltjes integral
Från Rilpedia
Riemann-Stieltjes integral, även kallad Stieltjesintegral, är inom matematisk analys en speciell integral, som kan ses som en generalisering av Riemannintegralen, uppkallad efter matematikern Thomas Joannes Stieltjes. Vid vanlig Riemannintegrering integrerar man med hänsyn till x-axeln, men vid Riemann-Stieltjes-integrering integrerar man med hänsyn till en annan funktion.
Innehåll |
Definition och existens
Konstruktion av integralen
Ett intervall av reella tal kallat [a,b] kan delas in i flera delintervall med en partition, P, som består av ändligt många punkter x0,x1,...,xn sådana att
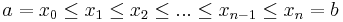 .
.
För två begränsade funktioner på intervallet, f(x) och α(x) inför vi differensoperatorn:
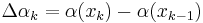 .
.
Då f(x) är begränsad på [a,b] kan vi hitta ett supremum respektive infimum för funktionsvärdena på dessa intervall och inför beteckningarna:
Vi får nu två summor, beroende på partitionen P och funktionerna f samt α:
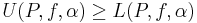 (då
(då 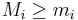 ).
).
Låt vidare 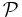 vara mängden av alla partitioner av [a,b] och om
vara mängden av alla partitioner av [a,b] och om
säger man att integralen existerar, vilket beteknas med 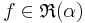 , och betecknar värdet med:
, och betecknar värdet med:
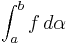 eller
eller 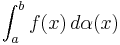 .
.
Om man väljer α(x) = x fås den vanliga Riemannintegralen.
Existens med epsilon
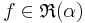 om och endast om det för varje ε > 0 existerar en partition P så att
om och endast om det för varje ε > 0 existerar en partition P så att
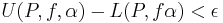 .
.
Egenskaper
För strängt ökande α och 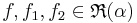 och
och 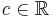 har integralen följande egenskaper:
har integralen följande egenskaper:
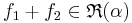 och
och 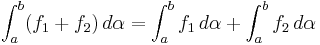 .
.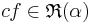 och
och 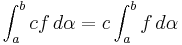 .
.- Om
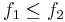 så
så 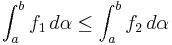 .
. - Om a < c < b så
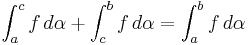
Om α1 och α2 är strängt ökande och 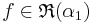 och
och 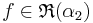 och
och 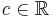 så:
så:
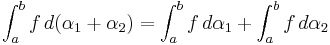 .
.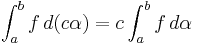
Om f även är kontinuerlig på hela [a,b] existerar det även ![c \in [a, b]](/w/images/sv.rilpedia.org/math/0/0/a/00a49aece4cc72157b51ca282347a0f8.png) så att:
så att:
vilket kallas medelvärdesegenskapen.
Om α är strängt ökande och kontinuerlig deriverbar på [a,b] och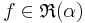 så är
så är
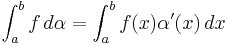 .
.
Tillämpningar
Riemann-Stieltjes integral kan användas till att räkna ut väntevärdet för en kumulativ fördelningsfunktion med diskret fördelning.