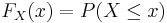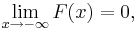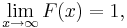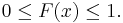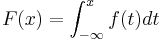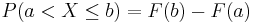Från Rilpedia

Den kumulativa fördelningsfunktionen beskriver en sannolikhetsfördelning för en slumpvariabel inom den matematiska statistiken. För en slumpvariabel X definierad på sannolikhetsrummet 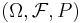så definieras den kumulativa fördelningsfunktionen F_X(x) som:

Med andra ord beskriver F_X(x) sannolikheten att X antar ett värde mindre än eller lika med x. Den kumulativa fördelningsfunktionen är monotont växande och högerkontinuerlig. Den har alltid följande egenskaper:

• 

• 

• 

För en diskret slumpvariabel som kan anta värdena x₁, x₂... är F diskontinuerlig i punkterna x_i och har konstant värde däremellan, d.v.s den har ett trappstegsliknande utseende.

För en kontinuerlig slumpvariabel är F en kontinuerlig funktion. Om F dessutom är absolutkontinuerlig så har vi sambandet

där f(t) är täthetsfunktionen (eller frekvensfunktionen) för variabelns fördelning.

Sannolikheten för att en slumpvariabel ska anta värden större än a och mindre eller lika med b kan beräknas med:

Tabell över värdena hos den kumulativa normalfördelningsfunktionen finns att läsa här. Andra fördelningar har andra tabeller.