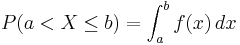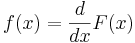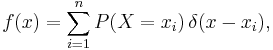Täthetsfunktion

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Täthetsfunktionen ger en bild av hur sannolika olika resultat är i förhållande till varandra till skillnad från fördelningsfunktionen som ger sannolikheten att komma till vänster om en given punkt x på talaxeln.


Innehåll

Kontinuerlig

För en kontinuerlig slumpvariabel (stokastisk variabel) beskriver täthetsfunktionen eller frekvensfunktionen, f, sannolikheten för att variabeln ska anta värden mellan a och b genom formeln

P(a<X\le b) = \int_a^b f(x)\,dx

Detta innebär att täthetsfunktionen matematiskt kan definieras som derivatan av den kumulativa fördelningsfunktionen F(X):

f(x) = \frac{d}{dx}F(x)

Diskret

f(x) = \sum_{i=1}^nP(X = x_i)\, \delta(x-x_i),

Krav

För att kunna beskriva en verklig sannolikhetsfördelning måste följande gälla för täthetsfunktionen:

  1. Ickenegativ på hela reella talxeln
  2. Integralen av den tagen över hela realaxeln måste bli 1.


Se även

Hämtad från "https://sv.rilpedia.org/wiki/T%C3%A4thetsfunktion"
Personliga verktyg