Generaliserad integral
Från Rilpedia
Innehåll |
Definition
En integral 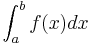 säges vara generaliserad om f(x) inte är definierad, är obegränsad i ett ändligt antal punkter och minst i en punkt på [a,b], eller om en integrationsgräns formellt ersatts med
säges vara generaliserad om f(x) inte är definierad, är obegränsad i ett ändligt antal punkter och minst i en punkt på [a,b], eller om en integrationsgräns formellt ersatts med 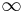 eller
eller 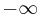 . En multipelintegral
. En multipelintegral 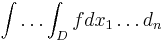 säges vara generaliserad om f är obegränsad, odefinierad i någon del av D, eller om D är obegränsad.
säges vara generaliserad om f är obegränsad, odefinierad i någon del av D, eller om D är obegränsad.
Betydelse
Antag att f(x) är definierad på intervallet [a,b[. Då definieras 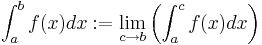 ,
, 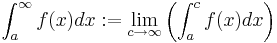 och
och 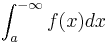 analogt. Alla generaliserade integraler kan överföras till en linjärkombination av de ovanstående tre integralerna. Om
analogt. Alla generaliserade integraler kan överföras till en linjärkombination av de ovanstående tre integralerna. Om 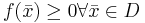 och
och 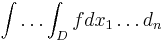 är generaliserad så definieras
är generaliserad så definieras 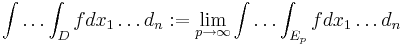 , där (En) är en uttömmande svit till D. Om f växlar tecken på D så definieras
, där (En) är en uttömmande svit till D. Om f växlar tecken på D så definieras 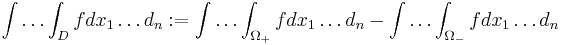 , där
, där 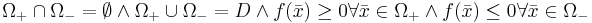 .
.
Konvergens
En generaliserad integral 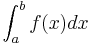 säges konvergera om gränsvärdet i definitionen av generaliserad integral existerar ändligt. Om integralen inte konvergerar säges den divergera.
säges konvergera om gränsvärdet i definitionen av generaliserad integral existerar ändligt. Om integralen inte konvergerar säges den divergera.



