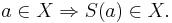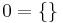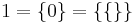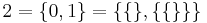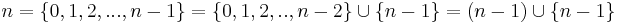Naturliga tal
Från Rilpedia
De naturliga talen är de heltal som inte är negativa (det vill säga 0, 1, 2, 3 och så vidare), alternativt de heltal som är positiva (alltså 1, 2, 3 och så vidare). Den förra definitionen är vanlig i Sverige och allmänt i matematisk logik, mängdlära och beräkningsvetenskap, medan den senare kan hittas i bland annat amerikansk litteratur och bland talteoretiker. Mängden av de naturliga talen betecknas 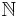 (ett vanligt N i fetstil kan även användas).
(ett vanligt N i fetstil kan även användas). 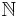 är diskret, uppräkneligt oändlig och har kardinalitet Alef-noll (
är diskret, uppräkneligt oändlig och har kardinalitet Alef-noll (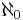 ).
).
Enligt den definition som görs i Matematikterminologi i skolan, utgiven av Statens skolverk i Sverige, ingår talet 0 bland de naturliga talen. Konventionen att räkna 0 bland de naturliga talen förekom inte alls före 1800-talet och tillämpas inte av alla matematiker. Den infördes i samband med att de naturliga talen gavs en mängdteoretisk definition, enligt vilken de naturliga talen precis motsvarar kardinaltalen för ändliga mängder och 0 måste användas som kardinaltal för den tomma mängden.
En fördel med att inkludera 0 är att de naturliga talen då utgör en monoid under både addition och multiplikation. En nackdel är att man inom talteori måste göra undantag för 0 i samband med primtalsfaktorisering, då 0 inte kan primtalsfaktoriseras (1 kan faktoriseras som den tomma produkten).
För att undvika förvirring kan 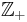 användas för att beteckna de positiva talen, och
användas för att beteckna de positiva talen, och 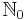 för de icke-negativa.
för de icke-negativa.
Formell definition
De naturliga talen kan konstrueras med Peanos axiom, det är även möjligt att konstruera dem utifrån mängdlära:
Låt 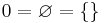 , den tomma mängden.
, den tomma mängden.
Definiera, för varje mängd a, funktionen 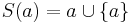 som ger efterföljaren till a.
som ger efterföljaren till a.
Om oändlighetsaxiomet gäller så existerar de naturliga talen och är snittet av alla mängder X som innehåller 0 och är slutna för S, dvs:
Denna mängd uppfyller Peanos axiom.
Ett naturligt tal kommer då vara mängden av alla tal som är mindre det:
då mängden n kommer att ha n element och n är mindre än eller lika med m om och endast om n är en delmängd till m.
Se även
Externa länkar
- Vad är ett naturligt tal? (PDF-fil 125kB)
Olika typer av matematiska tal
Naturliga tal - Heltal - Positiva tal - Noll - Negativa tal - Rationella tal - Irrationella tal - Reella tal - Algebraiska tal - Transcendent tal - Imaginära tal - Komplexa tal - Hyperkomplexa tal (Kvaternioner Oktonioner Sedenioner) - Perfekta tal